题目内容
3.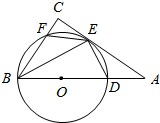 如图,△ABC是直角三角形,∠C为直角,D是斜边AB上一点,以BD为直径的圆O与AC相切于点E,与BC相交于点F.
如图,△ABC是直角三角形,∠C为直角,D是斜边AB上一点,以BD为直径的圆O与AC相切于点E,与BC相交于点F.(1)求证:BE2=BC•BD;
(2)若DE=6,CF=4,求AE的长.
分析 (1)结合弦切角定理,圆周角定理,及三角形相似的判定定理,可得△BEC∽△BDE,再由相似三角形的性质,得到BE2=BC•BD;
(2)若DE=6,CF=4,根据Rt△CFE∽Rt△EDB,△FEC∽△EBC,可得$sin∠CEF=sin∠CBE=\frac{2}{3}$,进而求出CE,BC,BE,BD的长,再由$\frac{AE}{AE+CE}=\frac{OE}{BC}=\frac{2}{3}$,可得答案.
解答 证明:(1)∵圆O与AC相切于点E,
∴∠BEC=∠BDE.
∵BD是圆O的直径,
∴∠BED=90°,
又∵∠C=90°,
∴△BEC∽△BDE----3
∴$\frac{BC}{BE}=\frac{BE}{BD}$
∴BE2=BC•BD------5
解:(2)∵∠CFE=∠EDB,
∴Rt△CFE∽Rt△EDB,
∴$\frac{CF}{DE}=\frac{CE}{BE}=\frac{2}{3}$,
∴$sin∠CBE=\frac{2}{3}$,
∵圆O与AC相切于点E,
∴△FEC∽△EBC,
∴$sin∠CEF=sin∠CBE=\frac{2}{3}$
∴EF=6,
∴$CE=\sqrt{E{F^2}-C{F^2}}=2\sqrt{5}$------7
又CE2=CF•CB,
∴BC=5,
∴BE2=CB2+CE2=45,
又∴BE2=BC•BD,
∴BD=9,
∴$OE=\frac{9}{2}$,
∵圆O与AC相切于点E,
∴OE⊥AC,
∴$\frac{AE}{AE+CE}=\frac{OE}{BC}=\frac{2}{3}$,即$\frac{AE}{{AE+2\sqrt{5}}}=\frac{{\frac{9}{2}}}{5}$,
∴$AE=18\sqrt{5}$------10
点评 本题考查的知识点是相似三角形的判定与性质,弦切角定理,圆周角定理,是平面几何的综合应用,难度较大.

| A. | 44 | B. | 45 | C. | 46 | D. | 47 |
 运行如图所示的程序框图,若输出结果为$\frac{6}{7}$,则判断框中应该填的条件是( )
运行如图所示的程序框图,若输出结果为$\frac{6}{7}$,则判断框中应该填的条件是( )| A. | k>5 | B. | k>6 | C. | k>7 | D. | k>8 |
| A. | p或q为真,非q为假 | B. | p或q为真,非p为真 | ||
| C. | p且q为假,非p为假 | D. | p且q为假,p或q为真 |
