题目内容
15.已知两直线l1:ax-by+4=0 l2:(a-1)x+y+b=0,求分别满足下列条件的a,b的值.(Ⅰ)直线l1过点(-3,-1),并且直线l1与直线l2垂直;
(Ⅱ)直线l1与直线l2平行,并且l1,l2在y轴上的截距互为相反数.
分析 (Ⅰ)由直线过点和直线垂直可得ab的方程组,解方程组可得;
(Ⅱ)由直线平行和截距互为相反数,ab的方程组,解方程组可得.
解答 解:(Ⅰ)∵直线l1过点(-3,-1),∴-3a+b+4=0 ①,
∵直线l1与直线l2垂直,∴a(a-1)+(-b)•1=0 ②
联立①②解得a=2,b=2;
(Ⅱ)∵直线l1与直线l2平行,∴a=-b(a-1),
又∵l1,l2在y轴上的截距互为相反数,
∴$\frac{4}{b}$=-(-b),解得b=2或b=-2,
当b=2时,可得a=$\frac{2}{3}$,当b=-2时,可得a=2
点评 本题考查直线的一般式方程和垂直关系,涉及直线的平行关系和直线的截距,属基础题.

练习册系列答案
相关题目
5.数列2,3,5,9,17,33,…的通项公式an可以是( )
| A. | 2n | B. | 2n+1 | C. | 2n-1 | D. | 2n-1+1 |
16.函数y=2sinx在区间[$\frac{π}{6}$,$\frac{4π}{3}$)的值域是( )
| A. | [-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | B. | (-$\sqrt{3}$,2] | C. | [$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$] | D. | [-$\sqrt{3}$,2) |
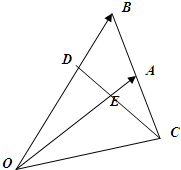 如图,已知△OAB中,点B关于点A的对称点为C,D在线段OB上,且OD=2DB,DC和OA相交于点E.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$.
如图,已知△OAB中,点B关于点A的对称点为C,D在线段OB上,且OD=2DB,DC和OA相交于点E.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$.