题目内容
【题目】设![]() 、
、![]() 是空间两条不同的直线,
是空间两条不同的直线,![]() 、
、![]() 是空间两个不同的平面.给出下列四个命题:
是空间两个不同的平面.给出下列四个命题:
①若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
③若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
④若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
其中正确的是__________(填序号).
【答案】②④
【解析】
利用空间中直线与直线的位置关系可判断命题①的正误;利用面面垂直的性质定理以及线面平行的判定定理可判断命题②的正误;利用线面垂直的性质可判断命题③的正误;利用面面垂直的性质定理和线面垂直的判定定理可判断命题④的正误.综合可得出结论.
对于命题①,若![]() ,
,![]() ,
,![]() ,则
,则![]() 与
与![]() 平行、相交或异面,命题①错误;
平行、相交或异面,命题①错误;
对于命题②,设![]() ,若
,若![]() ,则存在
,则存在![]() ,使得
,使得![]() ,则
,则![]() ,
,
又![]() ,则
,则![]() ,
,![]() ,
,![]() ,命题②正确;
,命题②正确;
对于命题③,![]() ,
,![]() ,则
,则![]() ,又
,又![]() ,则
,则![]() 或
或![]() ,命题③错误;
,命题③错误;
对于命题④,过直线![]() 作平面
作平面![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
![]() ,则
,则![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,命题④正确.
,命题④正确.
因此,正确命题的序号为②④.
故答案为:②④.

 全优点练单元计划系列答案
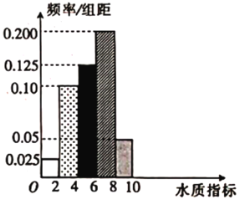
全优点练单元计划系列答案【题目】新《水污染防治法》已由中华人民共和国第十二届全国人民代表大会常务委员会第二十八次会议于2017年6月27日通过,自2018年1月1日起施行.2018年3月1日,某县某质检部门随机抽取了县域内100眼水井,检测其水质总体指标.
罗斯水质指数 | 02 | 24 | 46 | 68 | 810 |
水质状况 | 腐败污水 | 严重污染 | 污染 | 轻度污染 | 纯净 |
(1)求所抽取的100眼水井水质总体指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
(2)①由直方图可以认为,100眼水井水质总体指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在(5.21,5.99)内的概率;
落在(5.21,5.99)内的概率;
②将频率视为概率,若某乡镇抽查5眼水井的水质,记这5眼水井水质总体指标值位于(6,10)内的井数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100眼水井总体指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
【题目】国家规定每年的![]() 月
月![]() 日以后的
日以后的![]() 天为当年的暑假.某钢琴培训机构对
天为当年的暑假.某钢琴培训机构对![]() 位钢琴老师暑假一天的授课量进行了统计,如下表所示:
位钢琴老师暑假一天的授课量进行了统计,如下表所示:
授课量(单位:小时) |
|
|
|
|
|
频数 |
|
|
|
|
|
培训机构专业人员统计近![]() 年该校每年暑假
年该校每年暑假![]() 天的课时量情况如下表:
天的课时量情况如下表:
课时量(单位:天) |
|
|
|
|
|
频数 |
|
|
|
|
|
(同组数据以这组数据的中间值作代表)
(1)估计![]() 位钢琴老师一日的授课量的平均数;
位钢琴老师一日的授课量的平均数;
(2)若以(1)中确定的平均数作为上述一天的授课量.已知当地授课价为![]() 元/小时,每天的各类生活成本为
元/小时,每天的各类生活成本为![]() 元/天;若不授课,不计成本,请依据往年的统计数据,估计一位钢琴老师
元/天;若不授课,不计成本,请依据往年的统计数据,估计一位钢琴老师![]() 天暑假授课利润不少于
天暑假授课利润不少于![]() 万元的概率.
万元的概率.
【题目】某市教育局为了监控某校高一年级的素质教育过程,从该校高一年级16个班随机抽取了16个样本成绩,制表如下:
抽取次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
测评成绩 | 95 | 96 | 96 | 90 | 95 | 98 | 98 | 97 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
测评成绩 | 97 | 95 | 96 | 98 | 99 | 96 | 99 | 96 |
令![]() 为抽取的第
为抽取的第![]() 个学生的素质教育测评成绩,
个学生的素质教育测评成绩,![]() ,经计算得,
,经计算得,![]() ,
,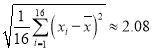 .以下计算精确到0.01.
.以下计算精确到0.01.
(1)设![]() 为抽取的16个样本的成绩,用频率估计概率,求
为抽取的16个样本的成绩,用频率估计概率,求![]() 的分布列、数学期望
的分布列、数学期望![]() 和标准方差
和标准方差![]() ;
;
(2)在抽取的样本成绩中,如果出现了在![]() 之外的成绩,就认为本学期的素质教育过程可能出现了异常情况,需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议.从该校抽样的结果来看,是否需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议?
之外的成绩,就认为本学期的素质教育过程可能出现了异常情况,需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议.从该校抽样的结果来看,是否需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议?
(3)列出不小于![]() 的所有样本成绩,设列出的这些成绩的中位数为
的所有样本成绩,设列出的这些成绩的中位数为![]() ,每次从列出的这些成绩中随机抽取1个成绩,有放回地连续抽取3次,求恰好有2次抽得的成绩为
,每次从列出的这些成绩中随机抽取1个成绩,有放回地连续抽取3次,求恰好有2次抽得的成绩为![]() 的概率.
的概率.
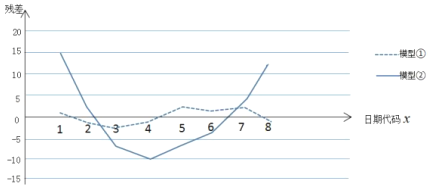
【题目】新型冠状病毒肺炎COVID-19疫情发生以来,在世界各地逐渐蔓延.在全国人民的共同努力和各级部门的严格管控下,我国的疫情已经得到了很好的控制.然而,小王同学发现,每个国家在疫情发生的初期,由于认识不足和措施不到位,感染人数都会出现快速的增长.下表是小王同学记录的某国连续8天每日新型冠状病毒感染确诊的累计人数.
日期代码x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
累计确诊人数y | 4 | 8 | 16 | 31 | 51 | 71 | 97 | 122 |
为了分析该国累计感染人数的变化趋势,小王同学打算从①![]() ,②
,②![]() 中选择一种模型对变量x和y的关系进行拟合,得到相应的回归方程,经过计算得
中选择一种模型对变量x和y的关系进行拟合,得到相应的回归方程,经过计算得![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
(1)请根据散点图,比较模型①,②的拟合效果,小王应该选择哪个模型?
(2)根据(1)问选定的模型求出相应的回归方程(系数均保留一位小数);
(3)由于时差,该国截止第9天新型冠状病毒感染确诊的累计人数尚未公布.小王同学认为,如果防疫形势没有得到明显改善,在数据公布之前可以根据他在(2)问求出的回归方程来对感染人数作出预测,那么估计该地区第9天新型冠状病毒感染确诊的累计人数是多少.
附:回归直线的最小二乘估计参考公式为: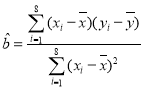 ,
,