题目内容
如图,在直四棱柱ABCDA1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,且AB=2CD,在棱AB上是否存在一点F,使平面C1CF∥平面ADD1A1?若存在,求点F的位置;若不存在,请说明理由.
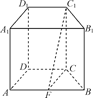

点F为AB的中点,
存在这样的点F,使平面C1CF∥平面ADD1A1,此时点F为AB的中点,证明如下:
∵AB∥CD,AB=2CD,∴AF綊CD,∴四边形AFCD是平行四边形.∴AD∥CF.
又AD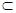 平面ADD1A1,CF
平面ADD1A1,CF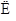 平面ADD1A1,
平面ADD1A1,
∴CF∥平面ADD1A1.
又CC1∥DD1,CC1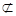 平面ADD1A1,DD1
平面ADD1A1,DD1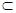 平面ADD1A1,∴CC1∥平面ADD1A1.
平面ADD1A1,∴CC1∥平面ADD1A1.
又CC1、CF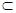 平面C1CF,CC1∩CF=C,
平面C1CF,CC1∩CF=C,
∴平面C1CF∥平面ADD1A1.
∵AB∥CD,AB=2CD,∴AF綊CD,∴四边形AFCD是平行四边形.∴AD∥CF.
又AD
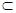 平面ADD1A1,CF
平面ADD1A1,CF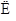 平面ADD1A1,
平面ADD1A1,∴CF∥平面ADD1A1.
又CC1∥DD1,CC1
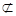 平面ADD1A1,DD1
平面ADD1A1,DD1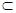 平面ADD1A1,∴CC1∥平面ADD1A1.
平面ADD1A1,∴CC1∥平面ADD1A1.又CC1、CF
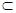 平面C1CF,CC1∩CF=C,
平面C1CF,CC1∩CF=C,∴平面C1CF∥平面ADD1A1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
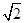 ,CE=EF=1.
,CE=EF=1.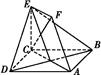

 与平面
与平面 平行的条件可以是( )
平行的条件可以是( )  ,直线b
,直线b ,且a//
,且a//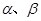 ,且
,且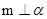 ,
,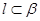 .给出下列命题:
.给出下列命题: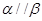 ,则
,则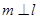 ;
;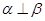 ,则
,则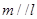 ;
;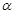 ,下列命题正确的是( )
,下列命题正确的是( ) 则
则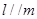
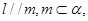 则
则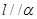
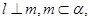 则
则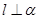
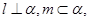 则
则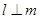
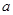 、
、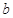 为不垂直的异面直线,
为不垂直的异面直线,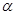 是一个平面,则
是一个平面,则