题目内容
袋中共有10个大小相同的编号为1、2、3的球,其中1号球有1个,2号球有3个,3号球有6个.
(1)从袋中任意摸出2个球,求恰好是一个2号球和一个3号球的概率;
(2)从袋中任意摸出2个球,记得到小球的编号数之和为 ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.
(1)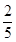 ;(2)
;(2)
解析试题分析:(1)从10个球中任意摸出2个基本事件总数为 个,摸出的恰好是一个2号球和一个3号球的基本事件数为
个,摸出的恰好是一个2号球和一个3号球的基本事件数为 ,根据古典概型概率公式即可求所求概率。(2)
,根据古典概型概率公式即可求所求概率。(2) 可能的取值为3,4,5,6。再求
可能的取值为3,4,5,6。再求 各取值的概率时方法同(1)仍属属古典概型概率,写出分布列后用期望公式直接求其期望值。
各取值的概率时方法同(1)仍属属古典概型概率,写出分布列后用期望公式直接求其期望值。
试题解析:(1)从袋中任意摸出2个球,恰好是一个2号球和一个3号球的概率为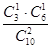 =
= .
.
(2) 可能的取值为3,4,5,6。
可能的取值为3,4,5,6。 ,
, ,
, ,
,
 的分布列为
的分布列为
3 4 5 6
P



 .
.
考点:1古典概型概率公式;2分布列及期望值。

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目


 表示抽到“幸福”的人数,求
表示抽到“幸福”的人数,求



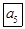 ,其中A的各位数中,a1=1,ak(k=2,3,4,5)出现0的概率为
,其中A的各位数中,a1=1,ak(k=2,3,4,5)出现0的概率为 ,出现1的概率为
,出现1的概率为 .记X=a1+a2+a3+a4+a5,当程序运行一次时,
.记X=a1+a2+a3+a4+a5,当程序运行一次时,