题目内容
5.对于任意|m|≤2的实数m,x∈(a,b),x2-mx-3<0恒成立,求b-a的最大值.分析 转化为以m为变量的函数形式,构造函数f(m)=x2-mx-3
解答 解:∵|m|≤2,∴-2≤m≤2,
则若对于任意|m|≤2的实数m,x∈(a,b),x2-mx-3<0恒成立,
设f(m)=x2-mx-3=(-x)m+x2-3,
则等价为$\left\{\begin{array}{l}{f(-2)<0}\\{f(2)<0}\end{array}\right.$,
即$\left\{\begin{array}{l}{2x+{x}^{2}-3<0}\\{{x}^{2}-2x-3<0}\end{array}\right.$,
即$\left\{\begin{array}{l}{-3<x<1}\\{-1<x<3}\end{array}\right.$,解得-1<x<1,
∵x∈(a,b),
∴当b=1,a=-1时,b-a取得最大值为1-(-1)=2.
点评 本题主要考查不等式恒成立,转化为m为主变量是解决本题的关键.

练习册系列答案
相关题目
6.设f(x)=|lgx|,若函数g(x)=f(x)-ax在区间(0,4)上有三个零点,则实数a的取值范围是( )
| A. | $({0,\frac{1}{e}})$ | B. | $({\frac{lg2}{2},\frac{lge}{e}})$ | C. | $({\frac{lg2}{2},e})$ | D. | $({0,\frac{lg2}{2}})$ |
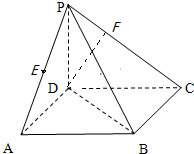 已知:如图在四梭椎P-ABCD中PD垂直于正方形ABCD所在的平面,E是AP的中点.
已知:如图在四梭椎P-ABCD中PD垂直于正方形ABCD所在的平面,E是AP的中点.