Question

已知实数x，y满足

x-2≤0 y-1≤0 x+2y-2≥0

，点P（x，y）在不等式组表示的平面区域上运动，则z=x-y的取值范围是

[-1，2]

．

Answer 1

分析：先作出不等式组表示的可行域，由z=x-y可得y=x-z，则-z为目标函数的纵截距，画直线y-x=0，平移可得直线过A或B时z有最值即可解决．

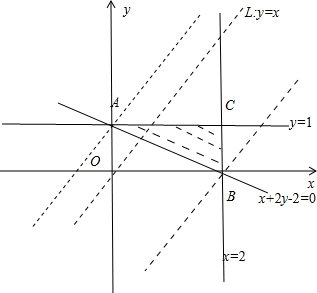
解答：解：画可行域如图，
由z=x-y可得y=x-z，则-z为直线y=x-z在y轴上的截距，截距越大，z越小
由

y=1 x+2y-2=0

可得A（0，1）；由

x=2 x+2y-2=0

可得B（2，0）
作直线L：y-x=0，平移直线过点A（0，1）时z有最小值-1；
平移直线过点B（2，0）时z有最大值2；
则z=y-x的取值范围是[-1，2]
故答案为：[-1，2]．

点评：本题主要考查了简单的线性规划，以及利用几何意义求最值，属于基础题．