题目内容
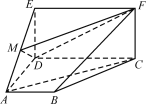
【题目】如图1,在矩形ABCD中,AB=4,AD=2,E,F,O分别为DC,AE,BC的中点.以AE为折痕把△ADE折起,使点D到达点P的位置,且平面PAE⊥平面ABCE(如图2).
(Ⅰ)求证:BC⊥平面POF;
(Ⅱ)求直线PA与平面PBC所成角的正弦值;
(Ⅲ)在线段PE上是否存在点M,使得AM∥平面PBC?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
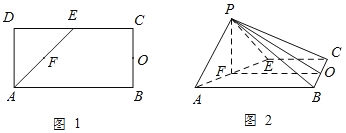
【答案】(Ⅰ)见解析;(Ⅱ)![]() ;(Ⅲ)见解析
;(Ⅲ)见解析
【解析】
(I)由面面垂直的性质定理得PF⊥平面ABCE,可得PF⊥BC,结合BC⊥OF,可得BC⊥平面POF;
(II)建立空间直角坐标系,计算平面PBC的法向量![]() ,通过计算法向量与
,通过计算法向量与![]() 的夹角得出线面角的正弦值;
的夹角得出线面角的正弦值;
(III)设![]() 则
则![]() ,令
,令![]() ,计算λ的值得出结论.
,计算λ的值得出结论.
(Ⅰ)在矩形ABCD中,AB=4,AD=2,E是CD中点,所以DA=DE,即PA=PE,
又F为AE的中点,所以PF⊥AE,又平面PAE⊥平面ABCE,平面PAE∩平面ABCE=AE,
PF平面PAE,所以PF⊥平面ABCE,BC平面ABCE,所以PF⊥BC,
由F,O分别为AE,BC的中点,易知FO∥AB,所以OF⊥BC,所以BC⊥平面POF,
(Ⅱ)过点O做平面ABCE的垂线OZ,以O为原点,分别以OF,OB,OZ为x,y,z轴建立坐标系O﹣xyz,
则![]()
∴![]() ,设平面PBC的法向量为
,设平面PBC的法向量为![]()
由 得
得![]() ,令z=3得
,令z=3得![]() ,
,
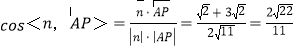 ,
,
所以直线PA与平面PBC所成角的正弦值![]() .
.
(Ⅲ)在线段PE上不存在点M,使得AM∥平面PBC.证明如下:
点M在线段PE上,设![]() 则
则![]() ,
,![]() ,
,
若AM∥平面PBC,则![]() ,
,
由![]() 得
得![]() ,解得λ=2[0,1]
,解得λ=2[0,1]
所以在线段PE上不存在点M,使得AM∥平面PBC.

【题目】某校学生会开展了一次关于“垃圾分类”问卷调查的实践活动,组织部分学生干部在几个大型小区随机抽取了共50名居民进行问卷调查.调查结束后,学生会对问卷结果进行了统计,并将其中一个问题“是否知道垃圾分类方法(知道或不知道)”的调查结果统计如下表:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
| 14 | 12 | 8 | 6 |
知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |
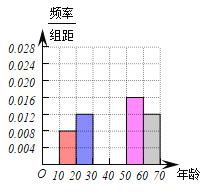
(1)求上表中的![]() 的值,并补全右图所示的的频率直方图;
的值,并补全右图所示的的频率直方图;
(2)在被调查的居民中,若从年龄在![]() 的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率.
的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率.
【题目】苹果是人们日常生活中常见的营养型水果.某地水果批发市场销售来自5个不同产地的富士苹果,各产地的包装规格相同,它们的批发价格(元/箱)和市场份额如下:
产地 |
|
|
|
|
|
批发价格 |
|
|
|
|
|
市场份额 |
|
|
|
|
|
市场份额亦称“市场占有率”.指某一产品的销售量在市场同类产品中所占比重.
(1)从该地批发市场销售的富士苹果中随机抽取一箱,求该箱苹果价格低于![]() 元的概率;
元的概率;
(2)按市场份额进行分层抽样,随机抽取![]() 箱富士苹果进行检验,
箱富士苹果进行检验,
①从产地![]() 共抽取
共抽取![]() 箱,求
箱,求![]() 的值;
的值;
②从这![]() 箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
(3)由于受种植规模和苹果品质的影响,预计明年产地![]() 的市场份额将增加
的市场份额将增加![]() ,产地
,产地![]() 的市场份额将减少
的市场份额将减少![]() ,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱
,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱![]() 元,明年苹果的平均批发价为每箱
元,明年苹果的平均批发价为每箱![]() 元,比较
元,比较![]() 的大小.(只需写出结论)
的大小.(只需写出结论)