题目内容
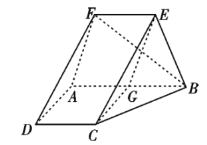
【题目】如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90,![]() ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC∥平面DMF,并说明理由;
(2)在(1)的条件下,求平面MDF将几何体ADE-BCF分成的两部分的体积之比.
【答案】(1)详见解析;(2)1:4.
【解析】
试题(1)要使得AC∥平面DMF,需要使得AC平行平面DMF内的一条直线.为了找这条直线,需要作一个过AC而与平面DMF相交的平面.为此,连结CE,交DF于N,连结MN,这样只要AC∥MN即可.因为N为线段DF的中点,所以只需M是线段AE的中点即可.
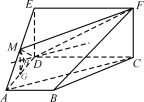
(2)一般地,求不规则的几何体的体积,可将其割为规则的几何体或补为规则的几何体.在本题中,可将几何体ADE-BCF补成三棱柱ADE-BCF,如图.这样利用柱体和锥体的体积公式即可得其体积之比.
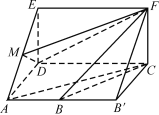
(1)当M是线段AE的中点时,AC∥平面DMF.
证明如下:
连结CE,交DF于N,连结MN,
由于M、N分别是AE、CE的中点,所以MN∥AC,
由于MN![]() 平面DMF,又AC
平面DMF,又AC![]() 平面DMF,
平面DMF,
所以AC∥平面DMF. 4分
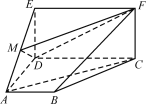
(2)如图,将几何体ADE-BCF补成三棱柱ADE-BCF,

三棱柱ADE-BCF的体积为![]() ,
,
则几何体ADE-BCF的体积
![]() =
=![]() .
.
三棱锥F-DEM的体积V三棱锥M-DEF=![]() ,
,
故两部分的体积之比为![]() (答14,4,41均可). 12分
(答14,4,41均可). 12分

【题目】随着科技的发展,近年看电子书的国人越来越多;所以近期有许多人呼呼“回归纸质书”,目前出版物阅读中纸质书占比出现上升现随机选出200人进行采访,经统计这200人中看纸质书的人数占总人数![]() .将这200人按年龄分成五组:第l组
.将这200人按年龄分成五组:第l组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,其中统计看纸质书的人得到的频率分布直方图如图所示.
,其中统计看纸质书的人得到的频率分布直方图如图所示.
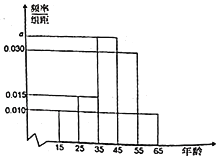
(1)求![]() 的值及看纸质书的人的平均年龄;
的值及看纸质书的人的平均年龄;
(2)按年龄划分,把年龄在![]() 的称青壮年组,年龄在
的称青壮年组,年龄在![]() 的称为中老年组,若选出的200人中看电子书的中老年人有10人,请完成下面
的称为中老年组,若选出的200人中看电子书的中老年人有10人,请完成下面![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下认为看书方式与年龄层有关?
列联表,并判断能否在犯错误的概率不超过0.1的前提下认为看书方式与年龄层有关?
看电子书 | 看纸质书 | 合计 | |
青壮年 | |||
中老年 | |||
合计 |
附:![]() (其中
(其中![]() ).
).
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |