题目内容
已知椭圆 的离心率为
的离心率为 ,且过点
,且过点 ,
, 为其右焦点.
为其右焦点.
(1)求椭圆 的方程;
的方程;
(2)设过点 的直线
的直线 与椭圆相交于
与椭圆相交于 、
、 两点(点
两点(点 在
在 两点之间),若
两点之间),若 与
与 的面积相等,试求直线
的面积相等,试求直线 的方程.
的方程.
(1)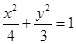 ;(2)
;(2)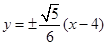 。
。
解析试题分析:(1)因为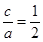 ,所以
,所以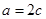 ,
,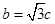 .
.
设椭圆方程为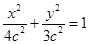 ,又点
,又点 在椭圆上,所以
在椭圆上,所以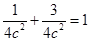 ,
,
解得 ,
,
所以椭圆方程为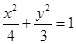 .
.
(2)易知直线 的斜率存在,
的斜率存在,
设 的方程为
的方程为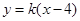 , 由
, 由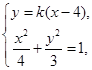 消去
消去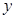 整理,得
整理,得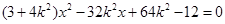 ,
,
由题意知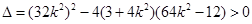 ,
,
解得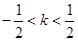 .
.
设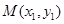 ,
,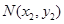 ,则
,则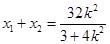 , ①,
, ①,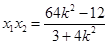 . ②.
. ②.
因为 与
与 的面积相等,
的面积相等,
所以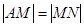 ,所以
,所以 . ③ 由①③消去
. ③ 由①③消去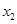 得
得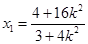 . ④
. ④
将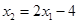 代入②得
代入②得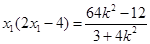 . ⑤
. ⑤
将④代入⑤ ,
,
整理化简得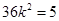 ,解得
,解得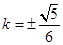 ,经检验成立.
,经检验成立.
所以直线 的方程为
的方程为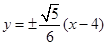 .
.
考点:椭圆的标准方程;椭圆的简单性质;直线与椭圆的综合应用。
点评:本题考查了椭圆方程的求法,以及直线与椭圆的综合应用,为圆锥曲线的常规题,应当掌握。考查了学生综合分析问题、解决问题的能力,知识的迁移能力以及运算能力。解题时要认真审题,仔细分析。

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
(本小题满分12分)
已知椭圆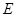 的中心在坐标原点、对称轴为坐标轴,且抛物线
的中心在坐标原点、对称轴为坐标轴,且抛物线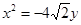 的焦点是它的一个焦点,又点
的焦点是它的一个焦点,又点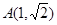 在该椭圆上.
在该椭圆上.
(1)求椭圆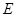 的方程;
的方程;
(2)若斜率为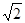 直线
直线 与椭圆
与椭圆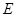 交于不同的两点
交于不同的两点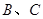 ,当
,当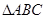 面积的最大值时,求直线
面积的最大值时,求直线 的方程.
的方程.
 方程为
方程为 ,左、右焦点分别是
,左、右焦点分别是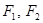 ,若椭圆
,若椭圆 到
到 .
.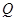 是椭圆
是椭圆 中点
中点 的轨迹方程;
的轨迹方程; 过定点
过定点 ,且与椭圆
,且与椭圆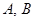 ,若
,若 为锐角(
为锐角( 为坐标原点),求直线
为坐标原点),求直线 的取值范围.
的取值范围. +
+ =1(a>b>0)的一个焦点是F(1,0),且离心率为
=1(a>b>0)的一个焦点是F(1,0),且离心率为 .
. 中,点
中,点 与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于
与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于 .
.
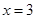 交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由。
交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由。 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.
 与抛物线C交于两点
与抛物线C交于两点 ,
, ,且
,且 (a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到
(a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到 .
. ),离心率为
),离心率为 .
.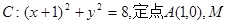 为圆上一动点,点
为圆上一动点,点 在
在 上,点
上,点 在
在 上,且满足
上,且满足 的轨迹为曲线
的轨迹为曲线 。
。
 求曲线
求曲线 若过定点F(0,2)的直线交曲线
若过定点F(0,2)的直线交曲线 (点
(点 在点
在点 之间),且满足
之间),且满足 ,求
,求 的取值范围。
的取值范围。