题目内容
【题目】如图,在四边形ABCD中,![]() ,_________,DC=2,在下面给出的三个条件中任选一个,补充在上面的问题中,并加以解答.(选出一种可行的方案解答,若选出多个方案分别解答,则按第一个解答记分)①
,_________,DC=2,在下面给出的三个条件中任选一个,补充在上面的问题中,并加以解答.(选出一种可行的方案解答,若选出多个方案分别解答,则按第一个解答记分)①![]() ;②
;②![]() ;③
;③![]() .
.
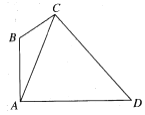
(1)求![]() 的大小;
的大小;
(2)求△ADC面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)若选①,利用正弦定理得出![]() ,再结合
,再结合![]() ,即可得出
,即可得出![]() ;
;
若选②,由![]() ,得出
,得出![]() ,再结合
,再结合![]() ,即可得出
,即可得出![]() ;
;
若选③,利用正弦定理的边化角公式化简得出得出![]() ,再结合
,再结合![]() ,即可得出
,即可得出![]() ;
;
(2)由余弦定理结合基本不等式得出![]() ,最后由三角形的面积公式得出△ADC面积的最大值.
,最后由三角形的面积公式得出△ADC面积的最大值.
(1)解:若选①在![]() ,由正弦定理可得:
,由正弦定理可得:![]()
又![]() ,可得:
,可得:![]()
又![]() ,
,![]() ,
,![]()
(2)在![]() 中,
中,![]() ,由余弦定理可得:
,由余弦定理可得:
![]()
即![]()
![]()
当且仅当![]() 时取“=”
时取“=”
若选择②
(1)由![]() 可得:
可得:![]()
又![]() ,
,![]()
(2)在![]() 中,
中,![]() ,由余弦定理可得:
,由余弦定理可得:
![]()
即![]()
![]()
当且仅当![]() 时取“=”.
时取“=”.
若选③(1)![]() ,由正弦定理得:
,由正弦定理得:
![]()
![]()
![]()
即![]()
![]()
![]()
![]()
![]()
又![]() ,所以
,所以![]() ;
;
(2)在![]() 中,
中,![]() ,由余弦定理可得:
,由余弦定理可得:
![]()
即![]()
![]()
当且仅当![]() 时取“=”
时取“=”

练习册系列答案
相关题目