��Ŀ����
�躯��f��x���Ķ�����ΪD�������ڷ���ʵ��hʹ�ö�������x��M��M⊆D������x+h⊆D����f��x+h����f��x�������f��x��ΪM�ϵġ�h�ߵ����������������½��ۣ�
��������f��x����R�ϵ�������������ڷ���ʵ��hʹf��x��ΪR�ϵġ�h�ߵ���������
��������f��x��ΪR�ϵġ�h�ߵ�����������f��x����R�ϵ���������
��������f��x��=x2Ϊ����[-1��+�ޣ��ϵġ�h������ƺ���������h��2��
��������f��x����R�ϵ��溯������x��0ʱ��f��x��=|x-1|-1����f��x��ֻ����R�ϵġ�4�ߵ���������
������ȷ���۵����Ϊ��������
��������f��x����R�ϵ�������������ڷ���ʵ��hʹf��x��ΪR�ϵġ�h�ߵ���������
��������f��x��ΪR�ϵġ�h�ߵ�����������f��x����R�ϵ���������
��������f��x��=x2Ϊ����[-1��+�ޣ��ϵġ�h������ƺ���������h��2��
��������f��x����R�ϵ��溯������x��0ʱ��f��x��=|x-1|-1����f��x��ֻ����R�ϵġ�4�ߵ���������
������ȷ���۵����Ϊ��������
��������Ϊ���ж��������٣�����ֻҪ�ܴ������Ƴ������������˵��Ϊ�����⣻ֻҪ�ܾٳ�����������˵����Ϊ�����⣬�����з������ĸ�����һһ��֤������������
����⣺���ڢ٣���Ϊ����f��x����R�ϵ������������Ա���Խ����ֵԽ�������¶��壮�����ڷ���ʵ��hʹf��x��ΪR�ϵġ�h�ߵ�����������Ϊ�����⣻
���ڢڣ��ٷ�����ͼ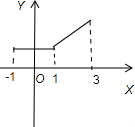 ������f��x���Ķ�����Ϊ[-1��3]��M=[-1��1]�������¶��壮�����ڷ���ʵ��2ʹf��x��ΪR�ϵġ�h�ߵ���������f��x����R�ϲ�������������Ϊ�����⣻
������f��x���Ķ�����Ϊ[-1��3]��M=[-1��1]�������¶��壮�����ڷ���ʵ��2ʹf��x��ΪR�ϵġ�h�ߵ���������f��x����R�ϲ�������������Ϊ�����⣻
���ڢۣ���Ϊ��������x��M��M⊆D������x+h⊆D����f��x+h����f��x������f��x+h����f��1��⇒x+h��1⇒h��1-x⇒h��2����Ϊ�����⣻
���ڢܣ���ͼ����ͼ��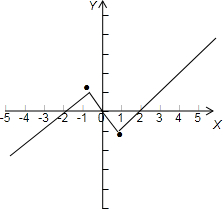 ��ͼ�ã�������ʵ��h�������㶨�壬����Ϊ�����⣮
��ͼ�ã�������ʵ��h�������㶨�壬����Ϊ�����⣮
��������ֻ�� �٢ۣ�
��ѡ A��
���ڢڣ��ٷ�����ͼ
 ������f��x���Ķ�����Ϊ[-1��3]��M=[-1��1]�������¶��壮�����ڷ���ʵ��2ʹf��x��ΪR�ϵġ�h�ߵ���������f��x����R�ϲ�������������Ϊ�����⣻
������f��x���Ķ�����Ϊ[-1��3]��M=[-1��1]�������¶��壮�����ڷ���ʵ��2ʹf��x��ΪR�ϵġ�h�ߵ���������f��x����R�ϲ�������������Ϊ�����⣻���ڢۣ���Ϊ��������x��M��M⊆D������x+h⊆D����f��x+h����f��x������f��x+h����f��1��⇒x+h��1⇒h��1-x⇒h��2����Ϊ�����⣻
���ڢܣ���ͼ����ͼ��
 ��ͼ�ã�������ʵ��h�������㶨�壬����Ϊ�����⣮
��ͼ�ã�������ʵ��h�������㶨�壬����Ϊ�����⣮��������ֻ�� �٢ۣ�
��ѡ A��
����������Ĺؼ����ڶԶ�������⣬ֻҪ����������������ͽ���ˣ���Ҳ����һ������Ŀ����Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
 ����b=f��
����b=f�� ���Ĵ�С��ϵΪ________��
���Ĵ�С��ϵΪ________�� ����b=f��
����b=f�� ���Ĵ�С��ϵΪ ��
���Ĵ�С��ϵΪ �� ����b=f��
����b=f�� ���Ĵ�С��ϵΪ�� ����
���Ĵ�С��ϵΪ�� ����