题目内容
10.给出下列四个结论:①函数y=sin(2x+$\frac{π}{3}$)的最小正周期是π;
②“(x-3)(x-4)=0”是“x-3=0”的充分不必要条件;
③命题“若m>0,则方程x2+x-m=0有实数根”的逆否命题为“若方程x2+x-m=0没有实数根,则m≤0”
④若 a>0,b>0,a+b=4,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为1.
其中正确结论的个数为①③④.
分析 求出三角函数的周期判断①;由充分必要条件的判定方法判断②;写出原命题的逆否命题判断③;利用基本不等式求出函数最值判断④.
解答 解:①函数y=sin(2x+$\frac{π}{3}$)的最小正周期是T=$\frac{2π}{2}$=π,①正确;
②由(x-3)(x-4)=0,得x-3=0或x-4=0,反之,由x-3=0,一定有(x-3)(x-4)=0,
∴“(x-3)(x-4)=0”是“x-3=0”的必要不充分条件,②错误;
③命题“若m>0,则方程x2+x-m=0有实数根”的逆否命题为“若方程x2+x-m=0没有实数根,则m≤0”,③正确;
④若a>0,b>0,a+b=4,则$\frac{1}{a}$+$\frac{1}{b}$=($\frac{1}{a}$+$\frac{1}{b}$)($\frac{a}{4}+\frac{b}{4}$)=$\frac{1}{2}+\frac{a}{4b}+\frac{b}{4a}≥\frac{1}{2}+2\sqrt{\frac{a}{4b}•\frac{b}{4a}}=1$,当且仅当a=b=2时等号成立,④正确.
故答案为:①③④.
点评 本题考查命题的真假判断与应用,考查了充分必要条件的判定方法,考查了三角函数周期的求法,训练了利用基本不等式求最值,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.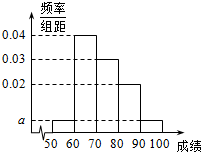 某校高二学生有800名,从中抽取100名学生期末考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]
某校高二学生有800名,从中抽取100名学生期末考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]
(Ⅰ)求图中α的值;
(Ⅱ)根据频率分布直方图,估计这100名学生语文成绩的平均分、中位数、众数;(精确到个位数)
(Ⅲ)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如表所示,求推测高二这800名学生中数学成绩在[50,90)之外的人数.
 某校高二学生有800名,从中抽取100名学生期末考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]
某校高二学生有800名,从中抽取100名学生期末考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100](Ⅰ)求图中α的值;
(Ⅱ)根据频率分布直方图,估计这100名学生语文成绩的平均分、中位数、众数;(精确到个位数)
(Ⅲ)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如表所示,求推测高二这800名学生中数学成绩在[50,90)之外的人数.
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
1.在平面直角坐标系中,O为坐标原点,P是由不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≥1}\end{array}\right.$所确定的平面区域内的动点,点Q是直线3x+4y-7=0上任意一点,O为坐标原点,则|$\overline{OP}+\overline{OQ}$|的最小值为( )
| A. | $\frac{7}{5}$ | B. | 2 | C. | $\frac{9}{5}$ | D. | $\frac{11}{5}$ |
5.从空间一点出发的三条射线PA,PB,PC均成60°角,则二面角B-PA-C的大小为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $arcsin\frac{1}{3}$ | D. | $arccos\frac{1}{3}$ |