题目内容
已知椭圆C的焦点在x轴,焦距为 ,F1,F2是椭圆的焦点,P为椭圆上一点,且|PF1|+|PF2|=4.
,F1,F2是椭圆的焦点,P为椭圆上一点,且|PF1|+|PF2|=4.
(Ⅰ)求此椭圆C的标准方程;
(Ⅱ)求证:直线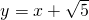 与椭圆C有且仅有一个公共点.
与椭圆C有且仅有一个公共点.
(Ⅰ)解:设椭圆方程为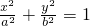 (a>b>0)
(a>b>0)
∴焦距为 ,|PF1|+|PF2|=4
,|PF1|+|PF2|=4
∴2c=2 ,2a=4
,2a=4
∴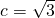 ,a=2
,a=2
∵b2=a2-c2=1
∴椭圆方程为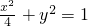 ;
;
(Ⅱ)证明:联立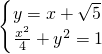 ,消去y整理得
,消去y整理得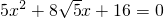
∵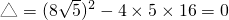
∴直线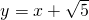 与椭圆C有且仅有一个公共点.
与椭圆C有且仅有一个公共点.
分析:(Ⅰ)利用椭圆C的焦点在x轴,焦距为 ,|PF1|+|PF2|=4,求出几何量,即可求得椭圆方程;
,|PF1|+|PF2|=4,求出几何量,即可求得椭圆方程;
(Ⅱ)直线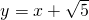 与椭圆联立,消去y整理得一元二次方程,利用判别式为0,可得结论.
与椭圆联立,消去y整理得一元二次方程,利用判别式为0,可得结论.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.
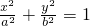 (a>b>0)
(a>b>0)∴焦距为
 ,|PF1|+|PF2|=4
,|PF1|+|PF2|=4∴2c=2
 ,2a=4
,2a=4∴
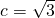 ,a=2
,a=2∵b2=a2-c2=1
∴椭圆方程为
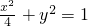 ;
;(Ⅱ)证明:联立
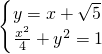 ,消去y整理得
,消去y整理得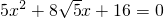
∵
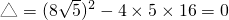
∴直线
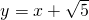 与椭圆C有且仅有一个公共点.
与椭圆C有且仅有一个公共点.分析:(Ⅰ)利用椭圆C的焦点在x轴,焦距为
 ,|PF1|+|PF2|=4,求出几何量,即可求得椭圆方程;
,|PF1|+|PF2|=4,求出几何量,即可求得椭圆方程;(Ⅱ)直线
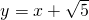 与椭圆联立,消去y整理得一元二次方程,利用判别式为0,可得结论.
与椭圆联立,消去y整理得一元二次方程,利用判别式为0,可得结论.点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目