题目内容
设函数 在
在 上的导函数为
上的导函数为 ,
, 在
在 上的导函数为
上的导函数为 ,若在
,若在 上,
上, 恒成立,则称函数
恒成立,则称函数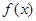 在
在 上为“凸函数”.已知当
上为“凸函数”.已知当 时,
时, 在
在 上是“凸函数”.则
上是“凸函数”.则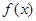 在
在 上 ( )
上 ( )
| A.既有极大值,也有极小值 | B.既有极大值,也有最小值 |
| C.有极大值,没有极小值 | D.没有极大值,也没有极小值 |
C
解析试题分析:根据已知中“凸函数”的概念可知,其两次求解导数后,导数为小于零的区间,即为凸函数的区间。由于当 时,
时, 在
在 上是“凸函数”.且有
上是“凸函数”.且有 ,则说明了
,则说明了 是x<m上的一个子区间,则可知不等式恒成立,结合极值的概念可知,有极大值,没有极小值,故选C.
是x<m上的一个子区间,则可知不等式恒成立,结合极值的概念可知,有极大值,没有极小值,故选C.
考点:本试题考查了函数的极值概念。
点评:对于极值的概念的理解是解决该试题的关键问题。极值是个局部概念,判定极值的方法可以通过在该点的导数值左正右负,或者左负右正来判定得到,属于基础题。

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
若方程 的根在区间
的根在区间 上,则
上,则 的值为( )
的值为( )
A. | B.1 |
C. 或2 或2 | D. 或1 或1 |
若对任意的 ,函数
,函数 满足
满足 ,且
,且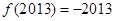 ,则
,则 ( )
( )
| A.0 | B.1 | C.-2013 | D.2013 |
已知函数 ( )
( )
A. | B. | C. | D. |
函数 的值域是( )
的值域是( )
A. | B. | C. | D. |
函数 在下列区间内一定有零点的是 ( )
在下列区间内一定有零点的是 ( )
| A.[0,1] | B.[1,2] | C.[2,3] | D.[3,4] |
 的图象的大致形状是
的图象的大致形状是 
 和
和 ,定义运算“
,定义运算“ ”:
”: .设函数
.设函数 ,
, .若函数
.若函数 的图象与
的图象与 轴恰有两个公共点,则实数
轴恰有两个公共点,则实数 的取值范围是( )
的取值范围是( )



 ,则函数
,则函数 的图象大致为( )
的图象大致为( )