题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点B(0,1).
,且过点B(0,1).

(Ⅰ)求椭圆的方程;
(Ⅱ)若点A是椭圆的右顶点,点![]() 在以AB为直径的圆上,延长PB交椭圆E于点Q,求
在以AB为直径的圆上,延长PB交椭圆E于点Q,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)由椭圆的离心率和b=1,结合基本量的关系,可得a,进而得到椭圆方程;(Ⅱ)由A(2,0),又B(0,1),求得圆方程和设PQ的参数方程为![]() (t为参数,α为锐角),分别代入圆方程和椭圆方程,可得|BP|,|BQ|,再由换元法和判别式法,解不等式可得最大值.
(t为参数,α为锐角),分别代入圆方程和椭圆方程,可得|BP|,|BQ|,再由换元法和判别式法,解不等式可得最大值.
(Ⅰ)椭圆![]() 的离心率为
的离心率为![]() ,且过点B(0,1),可得b=1,
,且过点B(0,1),可得b=1,![]() ,
,![]() ,解得a=2,
,解得a=2,![]() ,则椭圆E的方程为
,则椭圆E的方程为![]() ;
;
(Ⅱ)可得A(2,0),又B(0,1),可得以AB为直径的圆方程为![]() ,
,
设PQ的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为锐角),
为锐角),
代入圆方程可得![]() ,
,
可得![]() ,
,
将直线的参数方程代入椭圆方程可得:
![]() ,
,
可得![]() ,
,
则![]() ,
,
设![]() ,设上式为
,设上式为![]() ,
,
即有![]() ,
,
![]() ,即为
,即为![]() ,
,
解得![]() ,
,
则![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
【题目】已知某校5个学生期末考试数学成绩和总分年级排名如下表:
学生的编号 | 1 | 2 | 3 | 4 | 5 |
数学 | 115 | 112 | 93 | 125 | 145 |
年级排名 | 250 | 300 | 450 | 70 | 10 |
(1)通过大量事实证明发现,一个学生的数学成绩和总分年级排名具有很强的线性相关关系,在上述表格是正确的前提下,用![]() 表示数学成绩,用
表示数学成绩,用![]() 表示年级排名,求
表示年级排名,求![]() 与
与![]() 的回归方程;(其中
的回归方程;(其中![]() 都取整数)
都取整数)
(2)若在本次考试中,预计数学分数为120分的学生年级排名大概是多少?
参考数据和公式:![]() ,其中
,其中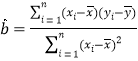 ,
,![]() ,其中
,其中![]()
