题目内容
(本小题满分12分)
已知直线 :
: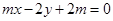
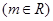 和椭圆
和椭圆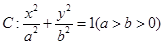 ,椭圆C的离心率为
,椭圆C的离心率为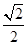 ,连结椭圆的四个顶点形成四边形的面积为
,连结椭圆的四个顶点形成四边形的面积为 .
.
(1)求椭圆C的方程;
(2)若直线 与椭圆C有两个不同的交点,求实数m的取值范围;
与椭圆C有两个不同的交点,求实数m的取值范围;
(3)当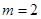 时,设直线
时,设直线 与y轴的交点为P,M为椭圆C上的动点,求线段PM长度的最大值.
与y轴的交点为P,M为椭圆C上的动点,求线段PM长度的最大值.
(1) ;(2)
;(2)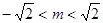 ;(3)|
;(3)|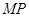 |取得最大值
|取得最大值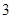 .
.
解析试题分析:本题主要考查椭圆的标准方程、直线与椭圆的相交问题、两点间的距离公式、配方法求函数最值等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,利用椭圆的标准方程,利用离心率求出基本量a和b,从而得到椭圆的标准方程;第二问,直线与椭圆方程联立,消参,由于直线与椭圆交于2个点,所以消参后的方程的判别式大于0,解不等式求出m的取值范围;第三问,将m=2代入,直接得到直线 的方程,从而得到p点坐标,设出p点坐标,则利用两点间距离公式可求出
的方程,从而得到p点坐标,设出p点坐标,则利用两点间距离公式可求出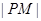 ,利用点M在椭圆上,转化x,通过配方法求函数的最值.
,利用点M在椭圆上,转化x,通过配方法求函数的最值.
(1)由离心率 ,得
,得
又因为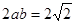 ,所以
,所以 ,
,
即椭圆标准方程为 . 4分
. 4分
(2)由  消
消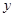 得:
得: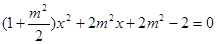 .
.
所以 , 可化为
, 可化为 
解得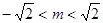 . 8分
. 8分
(3)由l: ,设
,设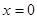 , 则
, 则 , 所以
, 所以 9分
9分
设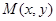 满足
满足 ,
,
则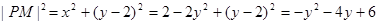 |
|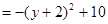
因为 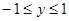 , 所以 11分
, 所以 11分
当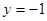 时,|
时,|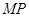 |取得最大值
|取得最大值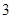 . 12分
. 12分
考点:椭圆的标准方程、直线与椭圆的相交问题、两点间的距离公式、配方法求函数最值.

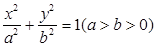 的左、右焦点分别为
的左、右焦点分别为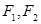 ,点
,点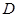 在椭圆上,
在椭圆上,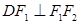 ,
,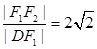 ,
,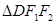 的面积为
的面积为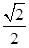 .
.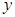 轴上的圆与椭圆在
轴上的圆与椭圆在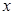 轴的上方有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径..
轴的上方有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径..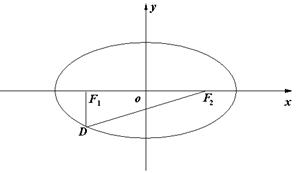
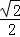 ,一条准线的方程是x=2
,一条准线的方程是x=2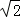
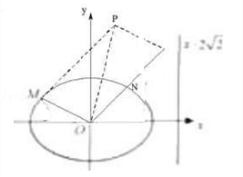
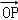 =
=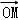 +2
+2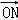 ,其中M、N是椭圆上的点,直线OM与ON的斜率之积为﹣
,其中M、N是椭圆上的点,直线OM与ON的斜率之积为﹣ ,
,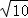 的距离之比为定值;若存在,求F的坐标,若不存在,说明理由.
的距离之比为定值;若存在,求F的坐标,若不存在,说明理由.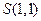 是抛物线为
是抛物线为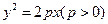 上的一点,以S为圆心,r为半径(
上的一点,以S为圆心,r为半径(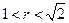 )做圆,分别交x轴于A,B两点,连结并延长SA、SB,分别交抛物线于C、D两点。
)做圆,分别交x轴于A,B两点,连结并延长SA、SB,分别交抛物线于C、D两点。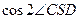 的值。
的值。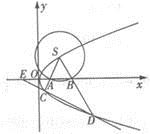
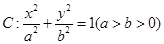 的左右焦点分别为
的左右焦点分别为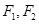 ,点
,点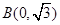 为短轴的一个端点,
为短轴的一个端点,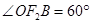 .
. 的方程;
的方程;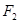 ,且斜率为
,且斜率为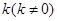 的直线
的直线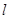 与椭圆
与椭圆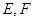 两点,
两点, 为椭圆的右顶点,直线
为椭圆的右顶点,直线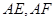 分别交直线
分别交直线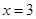 于点
于点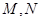 ,线段
,线段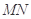 的中点为
的中点为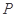 ,记直线
,记直线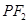 的斜率为
的斜率为 .
. 为定值.
为定值.
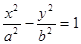 离心率是
离心率是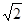 ,过点
,过点 ,且右支上的弦
,且右支上的弦 过右焦点
过右焦点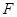 .
.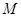 的轨迹E的方程;
的轨迹E的方程;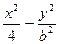 ="1"
="1" 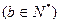 的两个焦点为
的两个焦点为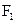 、
、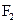 ,P是双曲线上的一点,
,P是双曲线上的一点,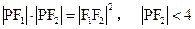 ,
,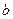 的值;
的值;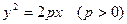 的焦点F与该双曲线的右顶点重合,斜率为1的直线经过点F与该抛物线交于A、B两点,求弦长|AB|.
的焦点F与该双曲线的右顶点重合,斜率为1的直线经过点F与该抛物线交于A、B两点,求弦长|AB|. ,过点
,过点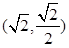 且离心率为
且离心率为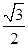 .
.
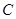 的方程;
的方程;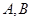 是椭圆
是椭圆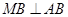 ,连接AM交椭圆于点P,在x轴上是否存在异于A、B的定点Q,使得直线BP和直线MQ垂直.
,连接AM交椭圆于点P,在x轴上是否存在异于A、B的定点Q,使得直线BP和直线MQ垂直.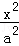 +
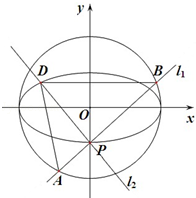
+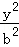 =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D.