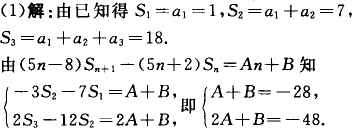题目内容
设数列{an}的前n项和为Sn,已知a1=1,a2=6,a3=11,且(5n-8)Sn+1-(5n+2)Sn=An+B,n=1,2,3,…,其中A、B为常数.
(1)求A与B的值;
(2)证明:数列{an}为等差数列;
(3)证明:不等式![]() >1对任何正整数m、n都成立.
>1对任何正整数m、n都成立.
答案:
解析:
提示:
解析:
|
解得A=-20,B=-8. (2)证法1:由(1)得(5n-8)Sn+1-(5n+2)Sn=-20n-8,① ∴(5n-3)Sn+2-(5n+7)Sn+1=-20n-28.② ②-①得(5n-3)Sn+2-(10n-1)Sn+1+(5n+2)Sn=-20,③ ∴(5n+2)Sn+3-(10n+9)Sn+2+(5n+7)Sn+1=-20.④ ④-③得(5n+2)Sn+3-(15n+6)Sn+2+(15n+6)·Sn+1-(5n+2)Sn=0. ∵an+1=Sn+1-Sn, ∴(5n+2)an+3-(10n+4)an+2+(5n+2)an+1=0. 又∵5n+2≠0, ∴an+3-2an+2+an+1=0, 即an+3-an+2=an+2-an+1,n≥1. 又a3-a2=a2-a1=5, ∴数列{an}为等差数列. 证法2:由已知,S1=a1=1, 又(5n-8)Sn+1-(5n+2)Sn=-20n-8,且5n-8≠0. ∴数列{Sn}是唯一确定的,因而数列{an}是唯一确定的.设bn=5n-4, |
提示:
|
主要考查等差数列的有关知识、不等式的证明方法,考查思维能力和运算能力. |

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目