题目内容
已知二次函数f(x)=x2+bx+c(x∈R),同时满足以下条件:①存在实数m,使得f(m)=0,且对任意实数x,恒有f(x)≥0成立;
②存在实数k (k≠0),使得f(1-k)=f(1+k)成立.
(1)求函数y=f(x)的解析式;
(2)设数列{an}的前n项和为Sn,Sn=f(n),数列{bn}满足关系式
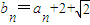 ,问数列{bn}中是否存在不同的3项,使之成为等比数列?若存在,试写出任意符合条件的3项;若不存在,请说明理由.
,问数列{bn}中是否存在不同的3项,使之成为等比数列?若存在,试写出任意符合条件的3项;若不存在,请说明理由.
【答案】分析:(1)二次函数有最小值0,二次函数的对称轴为直线x=1,求出b,c的值,即可求出函数y=f(x)的解析式
(2)根据Sn与an的关系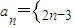
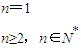 ,
,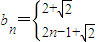
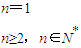 根据等比数列性质得出p、q、r的关系方程,研究方程的解的情况作出判断.
根据等比数列性质得出p、q、r的关系方程,研究方程的解的情况作出判断.
解答:解:(1)由①得,二次函数有最小值0,故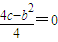 (2分)
(2分)
二次函数的对称轴为直线x=1,故 ,(4分)
,(4分)
即b=-2,c=1f(x)=x2-2x+1
(6分)
(2)Sn=n2-2n+1(n∈N*)∴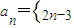
 (2分)
(2分)
∴
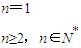 (4分)
(4分)
设数列的p、q、r(p<q<r)项使得bp、bq、br成等比数列.
(ⅰ)若p=1时,
 ,
,
则bq2=b1•br∴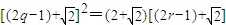 ∴
∴
∴
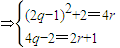 ①②
①②
由于②式左边为偶数,右边为奇数,显然q、r不存在. (3分)
(ⅱ)若1<p<r<q,p、q、r∈N*
则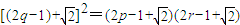 ∴
∴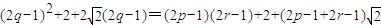
∴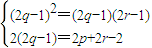 ⇒p+r=2q⇒(p+r-1)2=(2p-1)(2r-1)⇒(p-r)2=0
⇒p+r=2q⇒(p+r-1)2=(2p-1)(2r-1)⇒(p-r)2=0
∴p=r产生矛盾 (7分)
综上所述,这样的三项不存在. (8分)
点评:本题考查二次函数的性质,等比数列的定义,考查分析解决问题、分类讨论、计算等能力.
(2)根据Sn与an的关系
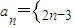
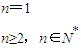 ,
,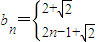
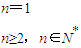 根据等比数列性质得出p、q、r的关系方程,研究方程的解的情况作出判断.
根据等比数列性质得出p、q、r的关系方程,研究方程的解的情况作出判断.解答:解:(1)由①得,二次函数有最小值0,故
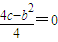 (2分)
(2分)二次函数的对称轴为直线x=1,故
 ,(4分)
,(4分)即b=-2,c=1f(x)=x2-2x+1
(6分)
(2)Sn=n2-2n+1(n∈N*)∴
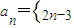
 (2分)
(2分)∴

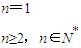 (4分)
(4分)设数列的p、q、r(p<q<r)项使得bp、bq、br成等比数列.
(ⅰ)若p=1时,

 ,
,
则bq2=b1•br∴
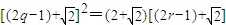 ∴
∴
∴

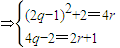 ①②
①②由于②式左边为偶数,右边为奇数,显然q、r不存在. (3分)
(ⅱ)若1<p<r<q,p、q、r∈N*
则
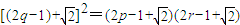 ∴
∴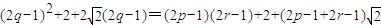
∴
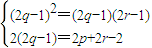 ⇒p+r=2q⇒(p+r-1)2=(2p-1)(2r-1)⇒(p-r)2=0
⇒p+r=2q⇒(p+r-1)2=(2p-1)(2r-1)⇒(p-r)2=0∴p=r产生矛盾 (7分)
综上所述,这样的三项不存在. (8分)
点评:本题考查二次函数的性质,等比数列的定义,考查分析解决问题、分类讨论、计算等能力.

练习册系列答案
相关题目