题目内容
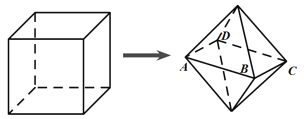
【题目】如图，棱长为1（单位：
）的正方体木块经过适当切割，得到几何体
，已知几何体由两个底面相同的正四棱锥组成，底面
平行于正方体的下底面，且各顶点均在正方体的面上，则几何体体积的取值范围是________（单位：
）．
【答案】
【解析】
根据图形可知几何体体积由正方形
面积来决定，根据截面正方形可知当
为四边中点时，面积最小；为正方形四个顶点时，面积最大，从而得到面积的取值范围；利用棱锥的体积公式可求得几何体的体积的取值范围.
由题意知，几何体中两个正四棱锥的高均为
，则几何体体积取值范围由正方形的面积来决定
底面平行于正方体底面，则可作所在截面的平面图如下：
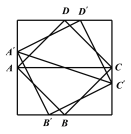
由正方形对称性可知，当为四边中点时，
取最小值；当为正方形四个顶点时，取最大值；
即
；
几何体
体积：
本题正确结果：
练习册系列答案
相关题目
