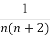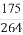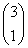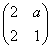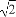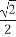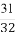Question

已知曲线C的极坐标方程为ρ2=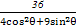,以极点为原点,极轴所在直线为x轴建立平面直角坐标系.

(1)求曲线C的直角坐标方程及参数方程.

(2)若P(x,y)是曲线C上的一个动点,求x+2y的最小值,并求P点的坐标.

 

Answer 1

(1) +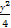=1 参数方程为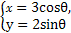(θ为参数) (2) P(-,-)

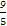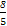【解析】(1)由ρ2=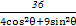得

4ρ2cos2θ+9ρ2sin2θ=36,

∴4x2+9y2=36,即+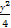=1,

化为参数方程为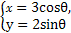(θ为参数).

(2)设P(3cosθ,2sinθ),

则x+2y=3cosθ+4sinθ=5sin(θ+φ),θ∈R,

∴当sin(θ+φ)=-1时,x+2y的最小值为-5,

此时,tanφ=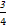,cosφ=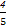,sin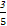φ=,θ+φ=,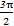

∴θ=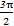-φ,sinθ=-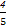,cosθ=-,

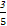∴P(-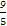,-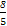)即为所求.