题目内容
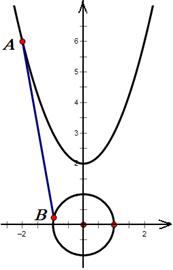
已知抛物线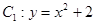 与圆
与圆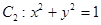
(I)求抛物线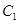 上一点
上一点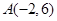 与圆
与圆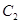 上一动点
上一动点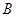 的距离的最小值;
的距离的最小值;
(II)将圆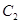 向上平移
向上平移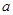 个单位后能否使圆
个单位后能否使圆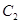 在抛物线
在抛物线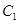 内并触及抛物线
内并触及抛物线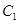 (与
(与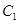 相切于顶点)的底部?若能,请求出
相切于顶点)的底部?若能,请求出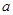 的值,若不能,试说明理由;
的值,若不能,试说明理由;
(III)设点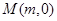 为
为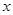 轴上一个动点,过
轴上一个动点,过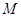 作抛物线
作抛物线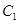 的两条切线,切点分别为
的两条切线,切点分别为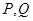 ,求证:直线
,求证:直线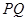 过定点,并求出定点坐标。
过定点,并求出定点坐标。
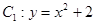 与圆
与圆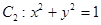
(I)求抛物线
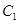 上一点
上一点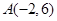 与圆
与圆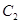 上一动点
上一动点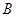 的距离的最小值;
的距离的最小值;(II)将圆
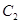 向上平移
向上平移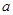 个单位后能否使圆
个单位后能否使圆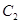 在抛物线
在抛物线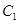 内并触及抛物线
内并触及抛物线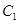 (与
(与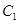 相切于顶点)的底部?若能,请求出
相切于顶点)的底部?若能,请求出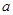 的值,若不能,试说明理由;
的值,若不能,试说明理由;(III)设点
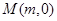 为
为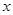 轴上一个动点,过
轴上一个动点,过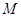 作抛物线
作抛物线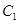 的两条切线,切点分别为
的两条切线,切点分别为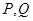 ,求证:直线
,求证:直线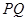 过定点,并求出定点坐标。
过定点,并求出定点坐标。
(1)所求最小值为 到圆心
到圆心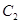 的距离减去圆的半径。即
的距离减去圆的半径。即
(2)假设平移后圆能触及抛物线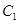 的底部,则
的底部,则 ,此时,圆方程为:
,此时,圆方程为: 与
与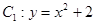 联立,可解得
联立,可解得 或
或 与题设矛盾。故满足条件的
与题设矛盾。故满足条件的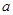 的值不存在。
的值不存在。
(3)设 ,由
,由 得切线
得切线 的方程为
的方程为 ,又
,又 ,
,
且直线 过点
过点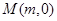 ,故
,故 ,故
,故 在直线
在直线 上
上
同理点 在直线
在直线 上,故直线
上,故直线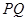 方程为
方程为 ,
,
即直线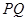 过定点
过定点
 到圆心
到圆心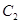 的距离减去圆的半径。即
的距离减去圆的半径。即
(2)假设平移后圆能触及抛物线
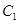 的底部,则
的底部,则 ,此时,圆方程为:
,此时,圆方程为: 与
与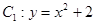 联立,可解得
联立,可解得 或
或 与题设矛盾。故满足条件的
与题设矛盾。故满足条件的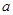 的值不存在。
的值不存在。(3)设
 ,由
,由 得切线
得切线 的方程为
的方程为 ,又
,又 ,
,且直线
 过点
过点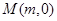 ,故
,故 ,故
,故 在直线
在直线 上
上同理点
 在直线
在直线 上,故直线
上,故直线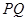 方程为
方程为 ,
,即直线
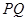 过定点
过定点
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 上运动,
上运动,



 上,过点P的直线
上,过点P的直线 与曲线C:
与曲线C: 只有一个公共点M,则
只有一个公共点M,则 的最小值为
的最小值为  为圆上一动点,点
为圆上一动点,点 在
在 上,点
上,点 在
在 上,且满足
上,且满足 的轨迹为曲线
的轨迹为曲线 .
. 与(1)中所求点
与(1)中所求点 是坐标原点,且
是坐标原点,且 ,求△
,求△ 的面积的取值范围.
的面积的取值范围.
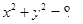 上动点,B(2,0),O为原点,那么
上动点,B(2,0),O为原点,那么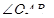 的最大值为
的最大值为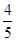 ,则cosa=_________.
,则cosa=_________.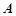 (-3,4)为圆心,且与
(-3,4)为圆心,且与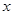 轴相切的圆的标准方程是 ▲
轴相切的圆的标准方程是 ▲  轴上,且与直线
轴上,且与直线 相切于点
相切于点 的圆的方程为____ ________________
的圆的方程为____ ________________