题目内容
有一种舞台灯,外形是正六棱柱,在其每一个侧面上安装5只颜色各异的彩灯,假若每只灯正常发光的概率为∴
≤
≤
.若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面.假定更换一个面需要100元,用ξ表示维修一次的费用.
(1)求恰好有2个面需要维修的概率;
(2)写出ξ的分布列,并求ξ的数学期望.
| 16 |
| 3 |
| 8 |
| 2k2+1 |
| 36 |
| 5 |
(1)求恰好有2个面需要维修的概率;
(2)写出ξ的分布列,并求ξ的数学期望.
分析:(Ⅰ)先求出一个面不需要维修的概率,从而得到一个面需要维修的概率.由此能够求出六个面中恰好有2个面需要维修的概率.
(Ⅱ)由ξ~B(6,
),知P6(0)=
=
,P6(1)=
=
,P6(2)=
=
,P6(3)=
=
,P6(4)=
=
,P6(5)=
=
,P6(6)=
=
,由此能得到维修一次的费用ξ的分布和ξ的数学期望.
(Ⅱ)由ξ~B(6,
| 1 |
| 2 |
| ||
| 26 |
| 1 |
| 64 |
| ||
| 26 |
| 3 |
| 32 |
| ||
| 26 |
| 15 |
| 64 |
| ||
| 26 |
| 5 |
| 16 |
| ||
| 26 |
| 15 |
| 64 |
| ||
| 26 |
| 3 |
| 32 |
| ||
| 26 |
| 1 |
| 64 |
解答:解:(Ⅰ)解:(Ⅰ)因为一个面不需要维修的概率为P5(3)+P5(4)+P5(5)=
=
,所以一个面需要维修的概率为
.
因此,六个面中恰好有2个面需要维修的概率为P6(2)=
=
.
(Ⅱ)因为ξ~B(6,
),又P6(0)=
=
,P6(1)=
=
,P6(2)=
=
,P6(3)=
=
,P6(4)=
=
,P6(5)=
=
,P6(6)=
=
,
所以维修一次的费用ξ的分布为:
…(12分)
因为ξ~B(6,
),所以Eξ=100×6×
=300元.
| ||||||
| 25 |
| 1 |
| 2 |
| 1 |
| 2 |
因此,六个面中恰好有2个面需要维修的概率为P6(2)=
| ||
| 26 |
| 15 |
| 64 |
(Ⅱ)因为ξ~B(6,
| 1 |
| 2 |
| ||
| 26 |
| 1 |
| 64 |
| ||
| 26 |
| 3 |
| 32 |
| ||
| 26 |
| 15 |
| 64 |
| ||
| 26 |
| 5 |
| 16 |
| ||
| 26 |
| 15 |
| 64 |
| ||
| 26 |
| 3 |
| 32 |
| ||
| 26 |
| 1 |
| 64 |
所以维修一次的费用ξ的分布为:
| ξ | 0 | 100 | 200 | 300 | 400 | 500 | 600 | ||||||||||||||
| P |
|
|
|
|
|
|
|
因为ξ~B(6,
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查离散型随机变量的数学期望和方差,解题时要注意二项分布的合理运用.

练习册系列答案
相关题目
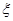 表示更换费用。
表示更换费用。