题目内容
有一种舞台灯,外形是正六棱柱ABCDEF-A1B1C1D1E1F1,在其每一个侧面上(不在棱上)安装5只颜色各异的彩灯,上下底面不安装彩灯,假若每只灯正常发光的概率是0.5,若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面.假定更换一个面需100元,用ξ表示维修一次的费用.(1)求侧面ABB1A1需要维修的概率;
(2)写出ξ的分布列,并求ξ的数学期望.
分析:(1)由题意知侧面ABB1A1需要维修包括三种结果,一是五个灯中有三个不发光,二是五个灯中有4个不发光,三是五个灯中有5个不发光,这三种结果是互斥的,而每一种结果又是一个独立重复试验,由公式得到结果.
(2)由题意知这个六棱柱每一个面要维修的概率是相同的,且各个面的维修情况是相互独立的,每次试验有两个结果,得到变量符合二项分布,根据二项分布的公式得到结果.
(2)由题意知这个六棱柱每一个面要维修的概率是相同的,且各个面的维修情况是相互独立的,每次试验有两个结果,得到变量符合二项分布,根据二项分布的公式得到结果.
解答:解:(1)由题意知侧面ABB1A1需要维修包括三种结果,
一是五个灯中有三个不发光,二是五个灯中有4个不发光,三是五个灯中有5个不发光,
这三种结果是互斥的,
而每一种结果又是一个独立重复试验,由公式得到
P1=
(
)5+
(
)5+
(
)5=
;
(2)∵由题意知这个六棱柱每一个面要维修的概率是相同的,
且各个面的维修情况是相互独立的,
∴ξ~B(6,
)
根据二项分布的公式得到
P6(0)=
,P6(1)=
,P6(2)=
,P6(3)=
,
P6(4)=
,P6(5)=
,P6(6)=
.
Eξ=100×6×
=300(元).
一是五个灯中有三个不发光,二是五个灯中有4个不发光,三是五个灯中有5个不发光,
这三种结果是互斥的,
而每一种结果又是一个独立重复试验,由公式得到
P1=
| C | 3 5 |
| 1 |
| 2 |
| C | 4 5 |
| 1 |
| 2 |
| C | 5 5 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵由题意知这个六棱柱每一个面要维修的概率是相同的,
且各个面的维修情况是相互独立的,
∴ξ~B(6,
| 1 |
| 2 |
根据二项分布的公式得到
P6(0)=
| 1 |
| 64 |
| 3 |
| 32 |
| 15 |
| 64 |
| 5 |
| 16 |
P6(4)=
| 15 |
| 64 |
| 3 |
| 32 |
| 1 |
| 64 |

Eξ=100×6×
| 1 |
| 2 |
点评:二项分布要满足的条件:每次试验中,事件发生的概率是相同的,各次试验中的事件是相互独立的,每次试验只要两种结果,要么发生要么不发生,随机变量是这n次独立重复试验中实件发生的次数.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
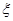 表示更换费用。
表示更换费用。