题目内容
上海世博会上有一种舞台灯,外形是正六边棱柱,在其每个侧面(编号分别是①②③④⑤⑥)上安装5只颜色各异的灯,每只灯正常发光的概率是0.5,若一侧面上至少有3只灯发光,则不需要更换这个面,否则需要更换这个面.
(1)求①号面需要更换的概率;
(2)求6个面上恰有2个面需要更换的概率.
(1)求①号面需要更换的概率;
(2)求6个面上恰有2个面需要更换的概率.
分析:(1)根据题意,分析可得若①号面需要更换,则①号面上的5个灯中至少有3只灯不能正常发光,包括有3只、4只、5只灯不能正常发光三种情况,由n次独立重复实验中恰有k次发生的概率公式计算可得每种情况的概率,相加可得答案;
(2)由(1)的结论,易得每个面需要更换的概率都为
,进而由n次独立重复实验中恰有k次发生的概率公式,计算可得答案.
(2)由(1)的结论,易得每个面需要更换的概率都为
| 1 |
| 2 |
解答:解:(1)①号面需要更换,即①号面上的5个灯中至少有3只灯不能正常发光,
有3只灯不能正常发光的概率为C53(
)3(
)2=10×(
)5
有4只灯不能正常发光的概率为C54(
)4(
)=5×(
)5
有5只灯不能正常发光的概率为C55(
)5=(
)5
则①号面需要更换的概率P=16×(
)5=
;
(2)由(1)的结论,易得每个面需要更换的概率都为
,
则6个面中恰有2个面需要更换的概率P=C62(
)4(
)2=15×(
)6=
.
有3只灯不能正常发光的概率为C53(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
有4只灯不能正常发光的概率为C54(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
有5只灯不能正常发光的概率为C55(
| 1 |
| 2 |
| 1 |
| 2 |
则①号面需要更换的概率P=16×(
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)的结论,易得每个面需要更换的概率都为
| 1 |
| 2 |
则6个面中恰有2个面需要更换的概率P=C62(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 64 |
点评:本题考查n次独立重复实验中恰有k次发生的概率计算,注意至少、最多、至少一类词的含义.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
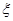 表示更换费用。
表示更换费用。 表示更换费用。
表示更换费用。