题目内容
已知函数,f(x)=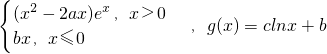 ,且
,且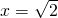 是函数y=f(x)的极值点.
是函数y=f(x)的极值点.
(1)若方程f(x)-m=0有两个不相等的实数根,求实数m的取值范围;
(2)若直线L是函数y=f(x)的图象在点(2,f(2))处的切线,且直线L与函数Y=G(X)的图象相切于点P(x0,y0),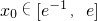 ,求实数b的取值范围.
,求实数b的取值范围.
解:(1)x>0时,f(x)=(x2-2ax)ex,
∴f'(x)=(2x-2a)ex+(x2-2ax)ex=[x2+2(1-a)x-2a]ex,
由已知,f′( )=0,∴[2+2
)=0,∴[2+2 (1-a)-2a]
(1-a)-2a]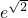 =0,
=0,
∴2+2 -2a-2
-2a-2 a=0,∴a=1,
a=0,∴a=1,
∴x>0时,f(x)=(x2-2x)ex,
∴f'(x)=(2x-2)ex+(x2-2x)ex=(x2-2)ex.
令f'(x)=0得x= (x=-
(x=- 舍去)
舍去)
当x>0时,
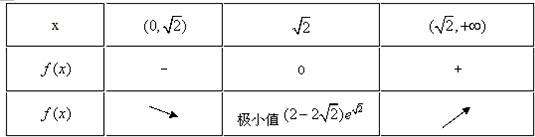
∴当 x∈(0, )时,f(x)单调递减,当 x∈(
)时,f(x)单调递减,当 x∈( ,+∞),f(x)单调递增,
,+∞),f(x)单调递增,
∴x>0时,f(x)∈((2-2 )
)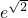 ,+∞)
,+∞)
要使方程f(x)-m=0有两不相等的实数根,即函数y=f(x)的图象与直线y=m有两个不同的交点.
①当b>0时,m=0或 m=(2-2 )
)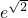 ;
;
②当b=0时,m∈((2-2 )
)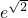 ,0);
,0);
③当b<0时,m∈((2-2 )
)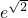 ,+∞)
,+∞)
(2)x>0时,f(x)=(x2-2x)ex,f'(x)=(x2-2)ex,∴f(2)=0,f'(2)=2e2.
函数f(x)的图象在点(2,f(2))处的切线l的方程为:y=2e2(x-2),
∵直线l与函数g(x)的图象相切于点P(x0,y0),x0∈[e-1,e],∴y0=clnx0+b,
∴切线l的斜率为 g′(x0)=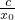
∴切线l的方程为:y-y0=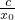 (x-x0),即y=
(x-x0),即y=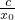 x-c+b+clnx0,
x-c+b+clnx0,
∴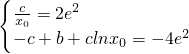 ,∴
,∴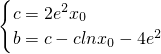
∴b=2e2(x0-x0lnx0-2),其中x0∈[e-1,e]
记h(x0)=2e2(x0-x0lnx0-2),其中x0∈[e-1,e],h'(x0)=-2e2lnx0,
令h'(x0)=0,得x0=1.
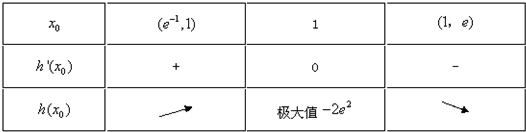
又h(e)=-4e2,h(e-1)=4e-4e2>-4e2.
∵x0∈[e-1,e],∴h(x0)∈[-4e2,-2e2],
∴实数b的取值范围为:{b|-4e2≤b≤-2e2}.
分析:(1)先求出其导函数,利用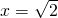 是函数y=f(x)的极值点,求出a的值;函数y=f(x)-m有两个零点,转化为函数y=f(x)的图象与直线y=m有两个不同的交点,利用导函数求出函数y=f(x)的单调区间,从而求出实数m的取值范围;
是函数y=f(x)的极值点,求出a的值;函数y=f(x)-m有两个零点,转化为函数y=f(x)的图象与直线y=m有两个不同的交点,利用导函数求出函数y=f(x)的单调区间,从而求出实数m的取值范围;
(2)利用导函数分别求出两个函数的切线方程,利用方程相等,对应项系数相等即可求出关于实数b的等式,再借助于其导函数即可求出实数b的取值范围.
点评:本题考查导数知识的运用,考查函数的极值,考查函数的单调性,考查函数与方程思想,属于中档题.
∴f'(x)=(2x-2a)ex+(x2-2ax)ex=[x2+2(1-a)x-2a]ex,
由已知,f′(
 )=0,∴[2+2
)=0,∴[2+2 (1-a)-2a]
(1-a)-2a]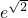 =0,
=0,∴2+2
 -2a-2
-2a-2 a=0,∴a=1,
a=0,∴a=1,∴x>0时,f(x)=(x2-2x)ex,
∴f'(x)=(2x-2)ex+(x2-2x)ex=(x2-2)ex.
令f'(x)=0得x=
 (x=-
(x=- 舍去)
舍去)当x>0时,

∴当 x∈(0,
 )时,f(x)单调递减,当 x∈(
)时,f(x)单调递减,当 x∈( ,+∞),f(x)单调递增,
,+∞),f(x)单调递增,∴x>0时,f(x)∈((2-2
 )
)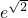 ,+∞)
,+∞)要使方程f(x)-m=0有两不相等的实数根,即函数y=f(x)的图象与直线y=m有两个不同的交点.
①当b>0时,m=0或 m=(2-2
 )
)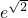 ;
;②当b=0时,m∈((2-2
 )
)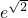 ,0);
,0);③当b<0时,m∈((2-2
 )
)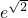 ,+∞)
,+∞)(2)x>0时,f(x)=(x2-2x)ex,f'(x)=(x2-2)ex,∴f(2)=0,f'(2)=2e2.
函数f(x)的图象在点(2,f(2))处的切线l的方程为:y=2e2(x-2),
∵直线l与函数g(x)的图象相切于点P(x0,y0),x0∈[e-1,e],∴y0=clnx0+b,

∴切线l的斜率为 g′(x0)=
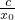
∴切线l的方程为:y-y0=
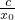 (x-x0),即y=
(x-x0),即y=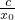 x-c+b+clnx0,
x-c+b+clnx0,∴
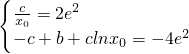 ,∴
,∴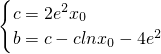
∴b=2e2(x0-x0lnx0-2),其中x0∈[e-1,e]
记h(x0)=2e2(x0-x0lnx0-2),其中x0∈[e-1,e],h'(x0)=-2e2lnx0,
令h'(x0)=0,得x0=1.

又h(e)=-4e2,h(e-1)=4e-4e2>-4e2.
∵x0∈[e-1,e],∴h(x0)∈[-4e2,-2e2],
∴实数b的取值范围为:{b|-4e2≤b≤-2e2}.
分析:(1)先求出其导函数,利用
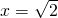 是函数y=f(x)的极值点,求出a的值;函数y=f(x)-m有两个零点,转化为函数y=f(x)的图象与直线y=m有两个不同的交点,利用导函数求出函数y=f(x)的单调区间,从而求出实数m的取值范围;
是函数y=f(x)的极值点,求出a的值;函数y=f(x)-m有两个零点,转化为函数y=f(x)的图象与直线y=m有两个不同的交点,利用导函数求出函数y=f(x)的单调区间,从而求出实数m的取值范围;(2)利用导函数分别求出两个函数的切线方程,利用方程相等,对应项系数相等即可求出关于实数b的等式,再借助于其导函数即可求出实数b的取值范围.
点评:本题考查导数知识的运用,考查函数的极值,考查函数的单调性,考查函数与方程思想,属于中档题.

练习册系列答案
相关题目
