题目内容
【题目】平面直角坐标系xOy中,过椭圆M: ![]() =1(a>b>0)焦点的直线x+y﹣2
=1(a>b>0)焦点的直线x+y﹣2 ![]() =0交M于P,Q两点,G为PQ的中点,且OG的斜率为9.
=0交M于P,Q两点,G为PQ的中点,且OG的斜率为9.
(1)求M的方程;
(2)A、B是M的左、右顶点,C、D是M上的两点,若AC⊥BD,求四边形ABCD面积的最大值.
【答案】
(1)解:设P(x1,y1),Q(x2,y2),G(x0,y0),则 ![]() ,
, ![]() ,
, ![]() ,
,
由此可得 ![]() ,因为x1+x2=2x0,y1+y2=2y0,
,因为x1+x2=2x0,y1+y2=2y0, ![]() ,所以
,所以 ![]() ,
,
又由题意知,M的一个焦点为 ![]() ,故a2﹣b2=8.因此a2=9,b2=1,
,故a2﹣b2=8.因此a2=9,b2=1,
所以M的方程为 ![]() .
.
(2)解:由题意可设直线AC的斜率为,所以直线AC的方程为y=k(x+1),
联立方程组 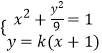 可得,(9+k2)x2+2k2x+k2﹣9=0,所以有
可得,(9+k2)x2+2k2x+k2﹣9=0,所以有 ![]() ,进而可得
,进而可得 ![]() ,所以
,所以 ![]() ,
,
同理可计算出 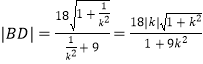 ,
,
所以四边形ABCD面积 ![]() ,
,
设 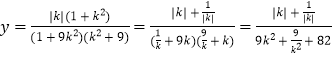 ,令
,令 ![]() (t≥2),所以
(t≥2),所以 ![]() ,此时
,此时 ![]() ,当且仅当
,当且仅当 ![]() 时取得等号,
时取得等号,
所以四边形ABCD面积的最大值为 ![]() .
.
【解析】(1)设P(x1,y1),Q(x2,y2),G(x0,y0),利用平方差法推出 ![]() ,通过M的一个焦点,求出a,b,即可求出M的方程.(2)由题意可设直线AC的斜率为,所以直线AC的方程为y=k(x+1),联立
,通过M的一个焦点,求出a,b,即可求出M的方程.(2)由题意可设直线AC的斜率为,所以直线AC的方程为y=k(x+1),联立 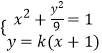 利用韦达定理以及弦长公式,求解四边形ABCD面积的表达式,通过换元法以及基本不等式求解最值即可.
利用韦达定理以及弦长公式,求解四边形ABCD面积的表达式,通过换元法以及基本不等式求解最值即可.

【题目】2017年3月27日,一则“清华大学要求从2017级学生开始,游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.游泳作为一项重要的求生技能和运动项目受到很多人的喜爱.其实,已有不少高校将游泳列为必修内容.某中学为了解2017届高三学生的性别和喜爱游泳是否有关,对100名高三学生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为 ![]() .
.
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.9%的把握认为喜欢游泳与性别有关?
附: ![]()
p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |