题目内容
【题目】在直角坐标系xOy中，设抛物线E：y2=2px（p＞0）的焦点为F，准线为直线l，点A、B在直线l上，点M为抛物线E第一象限上的点，△ABM是边长为 
的等边三角形，直线MF的倾斜角为60°．
（1）求抛物线E的方程；
（2）如图，直线m过点F交抛物线E于C、D两点，Q（2，0），直线CQ、DQ分别交抛物线E于G、H两点，设直线CD、GH的斜率分别为k1、k2 ， 求 
的值．
【答案】
（1）解：∵△ABM是边长为 
的等边三角形，∴|AB|=|AM|=|BMF|=4，
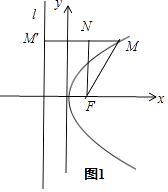
如图1，作MM′⊥l于点M′，FN⊥MM′于点N
由抛物线的定义知|MF|=|MM′|=4，
∵直线MF的倾斜角为60°，∴∠MFx=∠FMM′=600
所以|MN|=|MM′|﹣||NM′|=2，所以p=|MN|=2
所以抛物线E的方程y2=4x
（2）解：设直线CD的方程为x=my+1，C（x1，y1），D（x2，y2）
联立 
y2﹣4my﹣4=0
△=16m2+16＞0，y1+y2=4m，{y1y2=﹣4
因为点C在抛物线E：y2=4x上，所以点C的坐标 
，
所以kCQ= 
，
所以直线CQ的方程为：y﹣0= 
，即x= 
，
联立把x= 代入y2=4x，解得G（ 
）同理可得，H（ 
），
所以 
，
所以 
【解析】（1）由△ABM是边长为 的等边三角形，得|AB|=|AM|=|BMF|=4，如图1，作MM′⊥l于点M′，FN⊥MM′于点N，由抛物线的定义知|MF|=|MM′，由|MN|=|MM′|﹣||NM′|=2，得p=|MN|；（2）设直线CD的方程为x=my+1，C（x1，y1），D（x2，y2），联立 y2﹣4my﹣4=0得C的坐标 ，kCQ= ，写出直线CQ的方程，得G、H坐标即可．
