若{an}是一个以2为首项.-2为公比的等比数列.则数列{an2}的前n项的和Sn= ．题目和参考答案——青夏教育精英家教网—

题目内容

若{a_n}是一个以2为首项，-2为公比的等比数列，则数列{a_n²}的前n项的和S_n=______．

由等比数列的通项公式可得，a_n=2•（-2）^n-1
∴a_n²=4•4^n-1=4ⁿ
数列{a_n²}是以4为首项，以4为公比的等比数列
由等比数列的求和公式可得，Sn=

4(1-4n)

1-4

4(4n-1)

故答案为：

4(4n-1)

练习册系列答案

课课练与单元测试系列答案

已知椭圆C长轴的两个顶点为A（－2，0），B（2，0），且其离心率为.

（Ⅰ）求椭圆C的标准方程；

（Ⅱ）若N是直线x=2上不同于点B的任意一点，直线AN与椭圆C交于点Q，设直线QB与以NB为直径的圆的一个交点为M（异于点B），求证：直线NM经过定点．

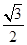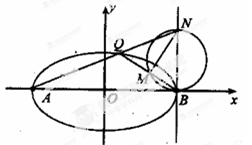
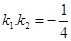在平面直角坐标系中，已知定点A（－2，0）、B（2，0），异于A、B两点的动点P满足，其中k₁、k₂分别表示直线AP、BP的斜率．

（Ⅰ）求动点P的轨迹E的方程；

（Ⅱ）若N是直线x=2上异于点B的任意一点，直线AN与（I）中轨迹E交予点Q，设直线QB与以NB为直径的圆的一个交点为M（异于点B），点C（1，0），求证：|CM|·|CN| 为定值．

试题分类