题目内容
已知椭圆C长轴的两个顶点为A(-2,0),B(2,0),且其离心率为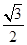 .
.
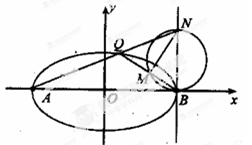
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若N是直线x=2上不同于点B的任意一点,直线AN与椭圆C交于点Q,设直线QB与以NB为直径的圆的一个交点为M(异于点B),求证:直线NM经过定点.
【答案】
(Ⅰ)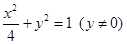 ;(Ⅱ)
;(Ⅱ)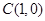 .
.
【解析】
试题分析:(Ⅰ)根据斜率公式,有斜率乘积等于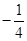 整理即得,注意
整理即得,注意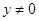 ;(Ⅱ)设直线
;(Ⅱ)设直线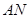 的方程,与椭圆方程组成方程组,消去
的方程,与椭圆方程组成方程组,消去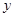 ,由韦达定理求点
,由韦达定理求点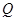 的坐标,根据直线
的坐标,根据直线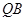 与以
与以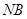 为直径的圆的另一个交点为
为直径的圆的另一个交点为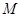 ,得
,得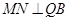 ,从而得到直线
,从而得到直线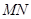 的方程,确定恒过的定点.
的方程,确定恒过的定点.
试题解析:(Ⅰ)设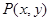 ,由
,由 得
得  ,其中
,其中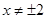 ,
,
整理得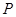 点的轨迹方程为
点的轨迹方程为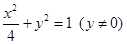 . (4分)
. (4分)
(Ⅱ)设点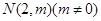 ,则直线
,则直线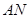 的方程为
的方程为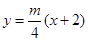 ,
,
解方程组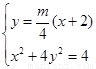 ,消去
,消去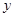 得
得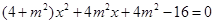 ,
,
设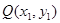 ,则
,则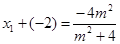 ,
,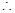
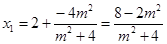 ,(8分)
,(8分)
从而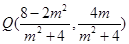 ,又
,又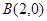 ,
,
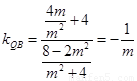
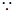 直线
直线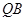 与以
与以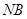 为直径的圆的另一个交点为
为直径的圆的另一个交点为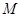 ,
,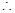
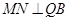 ,
,
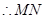 方程为
方程为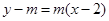 ,即
,即 ,过定点
,过定点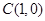 ,
(12分)
,
(12分)
考点:椭圆方程,直线与椭圆的关系,定点问题.

练习册系列答案
相关题目
 已知椭圆
已知椭圆 如图,已知:椭圆M的中心为O,长轴的两个端点为A、B,右焦点为F,AF=5BF.若椭圆M经过点C,C在AB上的射影为F,且△ABC的面积为5.
如图,已知:椭圆M的中心为O,长轴的两个端点为A、B,右焦点为F,AF=5BF.若椭圆M经过点C,C在AB上的射影为F,且△ABC的面积为5.