题目内容
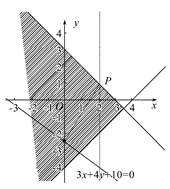
已知点P(2,t)在不等式组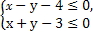 表示的平面区域内,则点P(2,t)到直线3x+4y+10=0距离的最大值为 .
表示的平面区域内,则点P(2,t)到直线3x+4y+10=0距离的最大值为 .
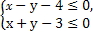 表示的平面区域内,则点P(2,t)到直线3x+4y+10=0距离的最大值为 .
表示的平面区域内,则点P(2,t)到直线3x+4y+10=0距离的最大值为 .4
因为点P(2,t)在可行域内,所以作出可行域,由图象可知,当点P在直线x+y-3=0上时,即P(2,1),此时点P到直线的距离最大为d=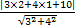 =
=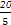 =4.
=4.
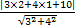 =
=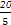 =4.
=4.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
题目内容
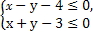 表示的平面区域内,则点P(2,t)到直线3x+4y+10=0距离的最大值为 .
表示的平面区域内,则点P(2,t)到直线3x+4y+10=0距离的最大值为 .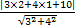 =
=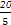 =4.
=4.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案