题目内容
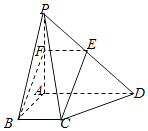
【题目】如图,PA⊥平面ABCD,AD∥BC,AD=2BC,AB⊥BC,点E为PD中点. 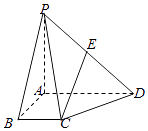
(1)求证:AB⊥PD;
(2)求证:CE∥平面PAB.
【答案】
(1)证明:∵PA⊥平面ABCD,AB平面ABCD,
∴PA⊥AB,
又∵AB⊥BC,AD∥BC,∴AB⊥AD,
又∵PA⊥AB,PA∩AD=A,
∴AB⊥平面PAD,
又PD平面PAD,∴AB⊥PD.
(2)证明:取PA的取中点F,连结EF∥AD,EF= ![]() AD,
AD,
又AD∥BC,AD=2BC,
∴EF∥BC,EF=BC,
∴四边形BCEF是平行四边形,∴EC∥BF,
∵EC平面PAB,BF平面PAB,
∴CE∥平面PAB.
【解析】(1)推导出PA⊥AB,AB⊥AD,由此能证明AB⊥平面PAD,从而AB⊥PD.(2)取PA的取中点F,连结EF∥AD,推导出四边形BCEF是平行四边形,从而EC∥BF,由此能证明CE∥平面PAB.
【考点精析】掌握直线与平面平行的判定和直线与平面垂直的性质是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;垂直于同一个平面的两条直线平行.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至11月份销售某种机械配件的销售量及销售单价进行了调查,销售单价x元和销售量y件之间的一组数据如表所示:
月份 | 7 | 8 | 9 | 10 | 11 |
销售单价x元 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y件 | 11 | 10 | 8 | 6 | 5 |
(1)根据7至11月份的数据,求出y关于x的回归直线方程;
(2)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润? 参考公式:回归直线方程 ![]() =b
=b ![]() +a,其中b=
+a,其中b= 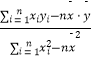 .
.
参考数据: ![]() =392,
=392, ![]() =502.5.
=502.5.