题目内容
4.函数f(1og2x)=x-$\frac{1}{x}$.(1)求f(x)的解析式;
(2)求证:函数f(x)为奇函数;
(3)若实数m满足:f(1-m)+f(1-m2)<0.求m的取值范围.
分析 (1)利用换元法求f(x)的解析式;
(2)利用奇函数的定义证明:函数f(x)为奇函数;
(3)利用函数的单调性、奇偶性,结合f(1-m)+f(1-m2)<0,求m的取值范围.
解答 (1)解:设t=1og2x,则x=2t,
∴f(t)=2t-2-t,
∴f(x)=2x-2-x;
(2)证明:∵f(-x)=2-x-2x=-(2x-2-x)=-f(x),
∴函数f(x)为奇函数;
(3)解:∵f(x)=2x-2-x,
∴f(x)=2x-2-x是增函数,
∵实数m满足:f(1-m)+f(1-m2)<0,
∴f(1-m)<f(-1+m2),
∴1-m<-1+m2,
∴m2+m-2>0,
∴m<-1或m>2.
点评 本题考查函数解析式的确定,考查函数的单调性、奇偶性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
14.函数y=ln(x2-x)+$\sqrt{4-{2^x}}$的定义域为( )
| A. | (1,+∞)∪(-∞,0) | B. | (1,2]∪(-∞,0) | C. | (-∞,0) | D. | (-∞,2] |
15.四人进行一项游戏,他们约定:在一轮游戏中,每人掷一枚质地均匀的骰子1次,若某人掷出的点数为5或6,则此人游戏成功.否则游戏失败.在一轮游戏中,至少有两人游戏成功的概率为( )
| A. | $\frac{1}{27}$ | B. | $\frac{8}{27}$ | C. | $\frac{11}{27}$ | D. | $\frac{8}{9}$ |
12.已知等比数列{an}中,a1-a3+a5=2,a3-a5+a7=5,那么a5-a7+a9=( )
| A. | 8 | B. | 15 | C. | 25 | D. | $\frac{25}{2}$ |
14.若数列an=$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$,则a5-a4=( )
| A. | $\frac{1}{10}$ | B. | -$\frac{1}{10}$ | C. | $\frac{1}{90}$ | D. | -$\frac{19}{90}$ |
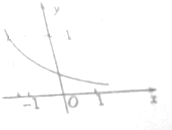 函数f(x)=ax-b的函数图象如图所示,其中a和b的取值范围是0<a<1,b<0.
函数f(x)=ax-b的函数图象如图所示,其中a和b的取值范围是0<a<1,b<0.