题目内容
方程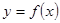 的曲线如图所示,那么方程
的曲线如图所示,那么方程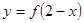 的曲线是( )
的曲线是( )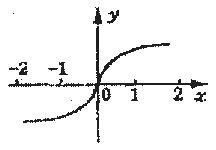
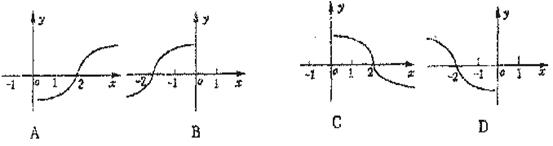
C
解析试题分析:跟据方程f(x,y)=0的曲线和方程f(2-x,y)=0的曲线中x系数互为相反数,作出函数f(x,y)=0关于y轴对称的函数的图象,曲线f(-x,y)和函数y=f(2-x,y)中x的系数不是1,故把-1提出,看x的变化,决定了左右平移的方向和平移的长度.
解:先作出f(x,y)=0关于y轴对称的函数的图象,
即为函数f(-x,y)=0的图象,
又f(2-x,y)=0即为f(-(x-2),y)=0,
即由f(-x,y)=0向右平移2个单位,故选C.
考点:函数图像的变换
点评:考查函数图象的平移变换对称变换和识图能力,注意左右平移时,不仅要注意作加右减,更要注意x的系数是否为1,不是1的时候,一定先提出系数,再平移,体现了数形结合和运动变化的思想,属基础题易错题.

练习册系列答案
相关题目
已知函数 ,
, ,且
,且 ,当
,当 时,
时, 是增函数,设
是增函数,设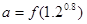 ,
,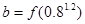 ,
, ,则
,则 、
、 、
、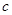 的大小顺序是( )。
的大小顺序是( )。
A. | B.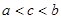 | C. | D. |
 ,若
,若 ,则
,则 =( )
=( )
A. | B. | C. | D. |
已知函数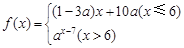 若数列{an}满足an=
若数列{an}满足an= (n∈N+)且{an}是递减数列,则实数a的取值范围是( )
(n∈N+)且{an}是递减数列,则实数a的取值范围是( )
A.( ,1) ,1) | B.( , ,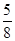 ) ) | C.( , ,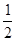 ) ) | D.(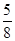 ,1) ,1) |
若函数 与函数
与函数 在区间
在区间 上都是减函数,则实数的取值范围为( )
上都是减函数,则实数的取值范围为( )
A. | B. | C. | D.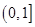 |
函数f(x)=xcosx在区间[0,2 ]上的零点个数为
]上的零点个数为
| A.2 | B.3 | C.4 | D.5 |
若定义在R上的偶函数 满足
满足 ,且当
,且当 时,
时, ,则函数
,则函数 的零点的个数为
的零点的个数为
| A.8 | B.6 | C.5 | D.4 |
如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成函数”。给出下列函数①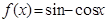 ;②
;②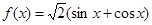 ;③
;③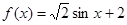 ;④
;④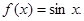 其中“互为生成函数”的是( )
其中“互为生成函数”的是( )
| A.①② | B.①③ | C.③④ | D.②④ |
已知 ,
, ,则有:( )
,则有:( )
A. | B. |
C. | D.以上都不是 |