题目内容
已知双曲线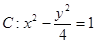 ,
,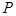 为
为 上任意一点;
上任意一点;
(1)求证:点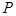 到双曲线
到双曲线 的两条渐近线的距离的乘积是一个常数;
的两条渐近线的距离的乘积是一个常数;
(2)设点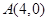 ,求
,求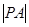 的最小值.
的最小值.
(1)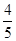 (2)
(2)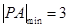
解析试题分析:(1)渐近线: ,设
,设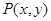 ,
,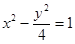
 到两条渐近线的距离乘积
到两条渐近线的距离乘积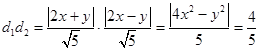
(2)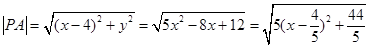 ,又
,又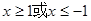
当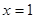 时,
时,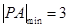
考点:双曲线的性质
点评:解决的关键是利用双曲线的性质来求解渐近线,以及结合函数的思想求解最值,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
已知双曲线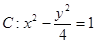 ,
,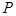 为
为 上任意一点;
上任意一点;
(1)求证:点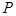 到双曲线
到双曲线 的两条渐近线的距离的乘积是一个常数;
的两条渐近线的距离的乘积是一个常数;
(2)设点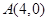 ,求
,求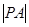 的最小值.
的最小值.
(1)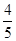 (2)
(2)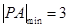
解析试题分析:(1)渐近线: ,设
,设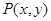 ,
,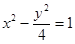
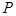 到两条渐近线的距离乘积
到两条渐近线的距离乘积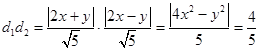
(2)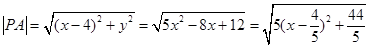 ,又
,又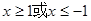
当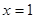 时,
时,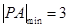
考点:双曲线的性质
点评:解决的关键是利用双曲线的性质来求解渐近线,以及结合函数的思想求解最值,属于基础题。

 阅读快车系列答案
阅读快车系列答案