题目内容
14.若数列{an}是公比为q的等比数列,证明:Sn+m=Sn+qnSm.分析 当公比q=1时,易得Sn+m=Sn+qnSm=(n+m)a1;当公比q≠1时,由求和公式代入验证可得Sn+m=Sn+qnSm=$\frac{{a}_{1}}{1-q}$(1-qn+m),综合可得.
解答 证明:当公比q=1时,有Sn=na1,
∴Sn+m=(n+m)a1,
Sn+qnSm=na1+1nma1=(n+m)a1,
∴Sn+m=Sn+qnSm;
当公比q≠1时,有Sn=$\frac{{a}_{1}}{1-q}$(1-qn),
∴Sn+m=$\frac{{a}_{1}}{1-q}$(1-qn+m),
Sn+qnSm=$\frac{{a}_{1}}{1-q}$(1-qn)+qn$\frac{{a}_{1}}{1-q}$(1-qm)
=$\frac{{a}_{1}}{1-q}$(1-qn+qn-qm+n)=$\frac{{a}_{1}}{1-q}$(1-qn+m),
∴Sn+m=Sn+qnSm.
综上可得Sn+m=Sn+qnSm
点评 本题考查等比数列的求和公式,涉及分类讨论的思想,属基础题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
18.设F1,F2分别为双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,若在双曲线右支上存在点P,满足|PF2|=|F1F2|,且F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\sqrt{2}$ | D. | 2 |
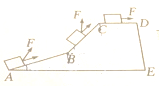 如图所示,一物体沿斜面在拉力F的作用下由A经B,C运动到D,其中AB=50m,BC=40m,CD=30m,变力F=$\left\{\begin{array}{l}{\frac{1}{4}x+5,0≤x≤90}\\{20,x>90}\end{array}\right.$(其中x为距离,单位:m,变力F的单位:N),在AB段运动时F与运动方向成30°角,在BC段运动时F与运动方向成45°,在CD段F与运动方向相同,求物体由A运动到D变力F所作的功W.
如图所示,一物体沿斜面在拉力F的作用下由A经B,C运动到D,其中AB=50m,BC=40m,CD=30m,变力F=$\left\{\begin{array}{l}{\frac{1}{4}x+5,0≤x≤90}\\{20,x>90}\end{array}\right.$(其中x为距离,单位:m,变力F的单位:N),在AB段运动时F与运动方向成30°角,在BC段运动时F与运动方向成45°,在CD段F与运动方向相同,求物体由A运动到D变力F所作的功W.