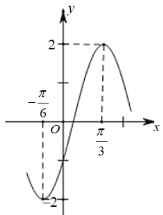
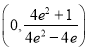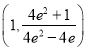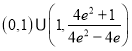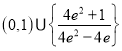题目内容
【题目】面积为2的![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,点
的中点,点![]() 在直线EF上,则
在直线EF上,则![]() 的最小值是( )
的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据△ABC的面积为2,可得△PBC的面积=1,从而可得PB×PC![]() ,故
,故![]() PB×PCcos∠BPC
PB×PCcos∠BPC![]() ,由余弦定理,有:BC2=BP2+CP2﹣2BP×CPcos∠BPC,进而可得BC2≥2BP×CP﹣2BP×CPcos∠BPC.
,由余弦定理,有:BC2=BP2+CP2﹣2BP×CPcos∠BPC,进而可得BC2≥2BP×CP﹣2BP×CPcos∠BPC.
从而![]() ,利用导数,可得
,利用导数,可得![]() 最大值为
最大值为![]() ,从而可得
,从而可得![]() 的最小值.
的最小值.
解:∵E、F是AB、AC的中点,∴EF到BC的距离=点A到BC的距离的一半,
∴△ABC的面积=2△PBC的面积,而△ABC的面积=2,∴△PBC的面积=1,
又△PBC的面积![]() PB×PCsin∠BPC,∴PB×PC
PB×PCsin∠BPC,∴PB×PC![]() .
.
∴![]() PB×PCcos∠BPC
PB×PCcos∠BPC![]() .
.
由余弦定理,有:BC2=BP2+CP2﹣2BP×CPcos∠BPC.
显然,BP、CP都是正数,∴BP2+CP2≥2BP×CP,∴BC2≥2BP×CP﹣2BP×CPcos∠BPC.
∴![]() PB×PCcos∠BPC+2BP×CP﹣2BP×CPcos∠BPC
PB×PCcos∠BPC+2BP×CP﹣2BP×CPcos∠BPC![]()
令y![]() ,则y′
,则y′![]()
令y′=0,则cos∠BPC![]() ,此时函数在(0,
,此时函数在(0,![]() )上单调增,在(
)上单调增,在(![]() ,1)上单调减
,1)上单调减
∴cos∠BPC![]() 时,
时,![]() 取得最大值为
取得最大值为![]()
∴![]() 的最小值是
的最小值是![]()
故选:D

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目