题目内容
【题目】在极坐标系中,已知曲线C1:ρ=2cosθ和曲线C2:ρcosθ=3,以极点O为坐标原点,极轴为x轴非负半轴建立平面直角坐标系.
(1)求曲线C1和曲线C2的直角坐标方程;
(2)若点P是曲线C1上一动点,过点P作线段OP的垂线交曲线C2于点Q,求线段PQ长度的最小值.
【答案】(1)C1的直角坐标方程为(x-1)2+y2=1,C2的直角坐标方程为x=3.(2)最小值为![]() .
.
【解析】
(1)根据题意,利用极坐标公式转化成直角坐标方程,即可求解,
(2)根据题意画出图像,则由圆几何性质可知PQ过点A(2,0),将直线的参数方程代入分别求参数,运用参数的几何意义求弦长,再根据基本不等式求解最值.
(1)C1的直角坐标方程为(x-1)2+y2=1,C2的直角坐标方程为x=3.
(2)设曲线C1与x轴异于原点的交点为A,
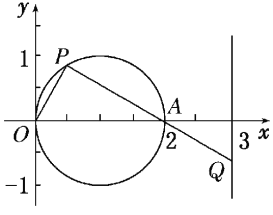
∵PQ⊥OP,∴PQ过点A(2,0),
设直线PQ的参数方程为![]() (t为参数),
(t为参数),
代入C1可得t2+2tcos θ=0,解得t1=0,t2=-2cos θ,
可知|AP|=|t2|=|2cos θ|.
代入C2可得2+tcos θ=3,解得t′=![]() ,
,
可知|AQ|=|t′|=![]() ,
,
∴|PQ|=|AP|+|AQ|=|2cos θ|+![]() ≥
≥![]() ,当且仅当|2cos θ|=
,当且仅当|2cos θ|=![]() 时取等号,
时取等号,
∴线段PQ长度的最小值为![]()

【题目】![]() 年初,新冠病毒引发的肺炎疫情在全球肆虐,为了有效地控制病毒的传播,某医院组织专家统计了该地区
年初,新冠病毒引发的肺炎疫情在全球肆虐,为了有效地控制病毒的传播,某医院组织专家统计了该地区![]() 名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如下图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.
名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如下图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.
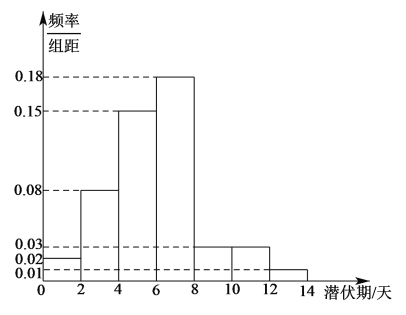
(1)求这![]() 名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表)和众数;
名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表)和众数;
(2)为研究潜伏期与患者年龄的关系,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有![]() 的把握认为潜伏期长短与患者年龄有关;
的把握认为潜伏期长短与患者年龄有关;
短潜伏者 | 长潜伏者 | 合计 | |
|
| ||
|
| ||
合计 |
|
(3)研究发现,某药物对新冠病毒有一定的抑制作用,需要从这![]() 人中分层选取
人中分层选取![]() 位
位![]() 岁以下的患者做Ⅰ期临床试验,再从选取的
岁以下的患者做Ⅰ期临床试验,再从选取的![]() 人中随机抽取两人做Ⅱ期临床试验,求两人中恰有
人中随机抽取两人做Ⅱ期临床试验,求两人中恰有![]() 人为“短潜伏者”的概率.
人为“短潜伏者”的概率.
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
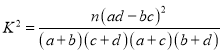 .
.