题目内容

已知双曲线的离心率为,左、右焦点分别为、,一条准线的方程为.

  (1)求双曲线的方程;

 

(2)若双曲线上的一点满足,求的值;

 (3)若直线与双曲线交于不同的两点,且在以为圆心的圆上,求实数的取值范围.

 (1)由条件有    ∴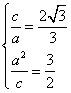

∴.

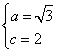
故双曲线的方程为:.

   (2)设.

∵    ∴

又   ∴

即.

又由余弦定理有:.

即    ∴.  故.

   (3)由

则由条件有:是     ①

设中点,则

又在为圆心的圆上. ∴.  

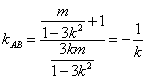
化简得:       ②

将②代入①得:解得.

又由    ∴

综上:或.

练习册系列答案
相关题目
已知双曲线的离心率为2，焦点是（-4，0），（4，0），则双曲线方程为（　　）
A、
x2
4
-
y2
12
=1
B、
x2
12
-
y2
4
=1
C、
x2
10
-
y2
6
=1
D、
x2
6
-
y2
10
=1
已知双曲线的离心率为2，F1、F2是左右焦点，P为双曲线上一点，且∠F1PF2=60°，S△PF1F2=12
3
．该双曲线的标准方程为
x2
4
-
y2
12
=1
x2
4
-
y2
12
=1
．
已知双曲线的离心率为2，焦点是（-4，0），（4，0），则双曲线方程为
x2
4
-
y2
12
=1
x2
4
-
y2
12
=1
．

（本小题满分12分）

已知双曲线的离心率为2，焦点到渐近线的距离等于，过右焦点的直线

 

交双曲线于、两点，为左焦点，

（Ⅰ）求双曲线的方程；

（Ⅱ）若的面积等于，求直线的方程．

 

已知双曲线的离心率为2，焦点到渐近线的距离为，点P的坐标为（0，－2），过P的直线l与双曲线C交于不同两点M、N.  

（1）求双曲线C的方程；

（2）设（O为坐标原点），求t的取值范围

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网