题目内容
13.已知函数$f(x)=sin(2x+\frac{π}{6})+\frac{1}{2}$.(Ⅰ)试用“五点法”画出函数f(x)在区间$[-\frac{π}{12},\frac{11π}{12}]$的简图;
(Ⅱ)指出该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?
(Ⅲ)若$x∈[-\frac{π}{6},\frac{π}{3}]$时,函数g(x)=f(x)+m的最小值为2,试求出函数g(x)的最大值并指出x取何值时,函数g(x)取得最大值.
分析 (Ⅰ)利用五点法,即将2x+$\frac{π}{6}$看成整体取正弦函数的五个关键点,通过列表、描点、连线画出函数图象;
(Ⅱ)用图象变换的方法得此函数图象,可以先向左平移,再横向伸缩,再向上平移的顺序进行;
(Ⅲ)g(x)=f(x)+m=sin(2x+$\frac{π}{6}$)+$\frac{1}{2}$+m,x∈[-$\frac{π}{6}$,$\frac{π}{3}$],求此函数的最值可先将2x+$\frac{π}{6}$看成整体,求正弦函数的值域,最后利用函数g(x)=f(x)+m的最小值为2,解方程可得m的值,进而求出函数最大值.
解答 解:(Ⅰ)先列表,再描点连线,可得简图.
| x | -$\frac{π}{12}$ | $\frac{2π}{12}$ | $\frac{5π}{12}$ | $\frac{8π}{12}$ | $\frac{11π}{12}$ |
| 2x+$\frac{π}{6}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| sin(2x+$\frac{π}{6}$) | 0 | 1 | 0 | -1 | 0 |
| y | $\frac{1}{2}$ | $\frac{3}{2}$ | $\frac{1}{2}$ | -$\frac{1}{2}$ | $\frac{1}{2}$ |
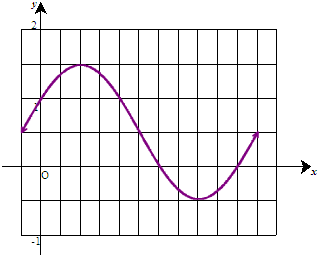
(Ⅱ)y=sinx向左平移$\frac{π}{6}$得到y=sin(x+$\frac{π}{6}$),
再保持纵坐标不变,横坐标缩短为原为的$\frac{1}{2}$变为y=sin(2x+$\frac{π}{6}$),
最后再向上平移$\frac{1}{2}$个单位得到y=sin(2x+$\frac{π}{6}$)+$\frac{1}{2}$.
(Ⅲ)g(x)=f(x)+m=sin(2x+$\frac{π}{6}$)+$\frac{1}{2}$+m,
∵x∈[-$\frac{π}{6}$,$\frac{π}{3}$],
∴2x+$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],
∴sin(2x+$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],
∴g(x)∈[m,$\frac{3}{2}$+m],
∴m=2,
∴gmax(x)=$\frac{3}{2}$+m=$\frac{7}{2}$,当2x+$\frac{π}{6}$=$\frac{π}{2}$即x=$\frac{π}{6}$时g(x)最大,最大值为$\frac{7}{2}$.
点评 本题综合考察了三角变换公式的运用,三角函数的图象画法,三角函数图象变换,及复合三角函数值域的求法.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
3.某校天文兴趣小组共有学生100人,其中一年级40人,二、三年级各30人,现要利用随机抽样的方法抽取10人参加某项调查,考虑选用简单随机抽样、系统抽样和分层抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为00,01,02,…,99;使用系统抽样时,将学生统一随机编号00,01,02,…,99,
并将整个编号依次分为10段.如果抽得号码有下列四种情况:
①05,10,17,36,47,53,65,76,90,95; ②05,15,25,35,45,55,65,75,85,95;
③08,17,42,48,52,56,61,64,74,88; ④08,15,22,29,48,55,62,78,85,92.
关于上述随机样本的下列结论中,正确的是( )
并将整个编号依次分为10段.如果抽得号码有下列四种情况:
①05,10,17,36,47,53,65,76,90,95; ②05,15,25,35,45,55,65,75,85,95;
③08,17,42,48,52,56,61,64,74,88; ④08,15,22,29,48,55,62,78,85,92.
关于上述随机样本的下列结论中,正确的是( )
| A. | ②、③都不能为系统抽样 | B. | ②、④都不能为分层抽样 | ||
| C. | ①、③都可能为分层抽样 | D. | ①、④都可能为分层抽样 |
18.若对?x,y∈(0,+∞),不等式4xlna<ex+y-2+ex-y-2+2恒成立,则正实数a的最大值是( )
| A. | $\sqrt{e}$ | B. | $\frac{1}{2}$e | C. | e | D. | 2e |