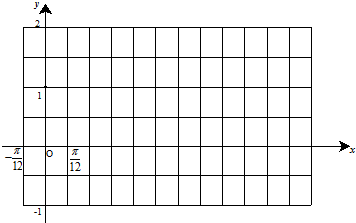
题目内容
5．证明对任意k，方程x2+（kx-2）2=$\frac{1}{{x}^{2}}$恒有解．分析 构造函数f（x）=x2+（kx-2）2-$\frac{1}{{x}^{2}}$，求导f′（x）=2x+2k（kx-2）+$\frac{2}{{x}^{3}}$，从而分类讨论以确定函数的单调性，并利用函数零点的判定定理求解即可．
解答 证明：构造函数f（x）=x2+（kx-2）2-$\frac{1}{{x}^{2}}$，
f′（x）=2x+2k（kx-2）+$\frac{2}{{x}^{3}}$，
①当k≤0时，若x＞0，则f′（x）＞0，
故f（x）在（0，+∞）上是增函数，
$\underset{lim}{x→{0}^{+}}$（x2+（kx-2）2-$\frac{1}{{x}^{2}}$）=-∞，
f（1）=1+（k-2）2-1=（k-2）2＞0，
故方程x2+（kx-2）2=$\frac{1}{{x}^{2}}$有解；
②当k＞0时，若x＜0，f′（x）＜0，
故f（x）在（0，+∞）上是减函数，
$\underset{lim}{x→{0}^{-}}$（x2+（kx-2）2-$\frac{1}{{x}^{2}}$）=-∞，
f（-1）=1+（-k-2）2-1=（-k-2）2＞0，
故方程x2+（kx-2）2=$\frac{1}{{x}^{2}}$有解；
综上所述，对任意k，方程x2+（kx-2）2=$\frac{1}{{x}^{2}}$恒有解．
点评 本题考查了导数的综合应用及分类讨论的思想应用．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
