题目内容
【题目】设函数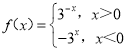
，若
，b＝f(log24.2)，c＝f(20.7)，则a，b，c的大小关系为( )
A.a＜b＜cB.b＜a＜cC.c＜a＜bD.c＜b＜a
【答案】A
【解析】
根据题意，分析可得f(x)为奇函数且在(0，+∞)上为减函数，由对数函数的性质比较可得1＜20.7＜2＜log24.2＜log25，结合函数的单调性分析可得答案．
当x＞0时，﹣x＜0，
f(x)＝3﹣x，f(﹣x)＝﹣3﹣x，
所以f(x)＝﹣f(﹣x)，
当x＜0时，﹣x＞0，
f(x)＝﹣3x，f(﹣x)＝3﹣(﹣x)＝3x，
所以f(x)＝﹣f(﹣x)，
所以函数f(x)是奇函数，且在(﹣∞，0)，(0，+∞)上单调递减．
所以a＝﹣f(log2
)＝f(﹣log2)＝f(log25)，
b＝f(log24.2)，c＝f(20.7)，
又1＜20.7＜2＜log24.2＜log25，
所以f(20.7)＞f(log24.2)＞f(log25)，
即a＜b＜c，
故选：A．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
