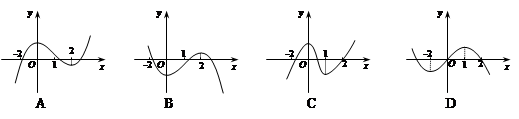题目内容
设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则f(-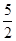 )= ( )
)= ( )
A.-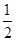 B.-
B.-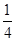 C .
C .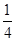 D.
D. 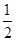
A
解析试题分析:解:∵f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),∴根据周期性可知,f(-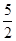 )=f(-
)=f(-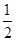 ),再利用奇函数性质可知 f(-
),再利用奇函数性质可知 f(-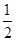 )=-f(
)=-f(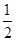 )=-
)=-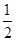 ,故答案为:A.
,故答案为:A.
考点:函数的周期性和奇偶性
点评:本题考查函数的周期性和奇偶性的应用,以及求函数的值.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
函数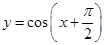 ,
,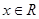 ( )
( )
| A.是偶函数 | B.是奇函数 |
| C.既不是奇函数也不是偶函数 | D.既是奇函数也是偶函数 |
定义在 上的偶函数
上的偶函数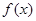 满足
满足 ,且在
,且在 上是减函数,
上是减函数, 是钝角三角形的两个锐角,则
是钝角三角形的两个锐角,则 与
与 的大小关系是
的大小关系是
A. | B. |
C. | D. |
若函数 的零点与
的零点与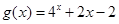 的零点之差的绝对值不超过
的零点之差的绝对值不超过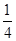 ,则
,则 可以是
可以是
A. =4x-1 =4x-1 | B. =(x-1)2 =(x-1)2 |
C. =ex-2 =ex-2 | D.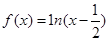 |
定义在 上的偶函数
上的偶函数 满足:对任意的
满足:对任意的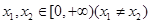 ,有
,有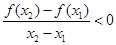 .则
.则
A.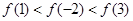 | B.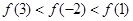 |
C.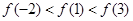 | D. |
若函数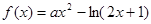 在区间
在区间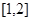 上为单调函数,则实数
上为单调函数,则实数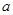 不可能取到的值为
不可能取到的值为
A.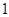 | B.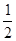 | C.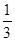 | D.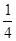 |
函数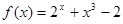 在区间(0,1)内的零点个数是 ( )
在区间(0,1)内的零点个数是 ( )
| A.0 | B.1 | C.2 | D.3 |
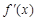 的图象如图所示,那么函数f (x)的图象最有可能的是( )
的图象如图所示,那么函数f (x)的图象最有可能的是( )