题目内容
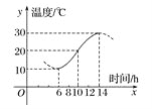
【题目】某城市在发展过程中，交通状况逐渐受到有关部门的关注，据有关统计数据显示，从上午6点到中午12点，车辆通过该市某一路段的用时y（分钟）与车辆进入该路段的时刻t之间的关系可近似地用如下函数给出： y=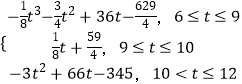 
求从上午6点到中午12点，通过该路段用时最多的时刻．
【答案】解：①当6≤t＜9时，
y′=﹣ 
t2﹣ 
t+36=﹣ （t+12）（t﹣8）
令y′=0，得t=﹣12（舍去）或t=8．
当6≤t＜8时，y′＞0，当8＜t＜9时，y′＜0，
故t=8时，y有最大值，ymax=18.75
②当9≤t≤10时，y= 
t+ 
是增函数，
故t=10时，ymax=16
③当10＜t≤12时，y=﹣3（t﹣11）2+18，
故t=11时，ymax=18
综上可知，通过该路段用时最多的时刻为上午8点
【解析】通过分段函数①当6≤t＜9时，利用函数的导数求出最大值；②当9≤t≤10时，通过函数的单调性求解最大值，③当10＜t≤12时，利用二次函数求解函数的最值，推出结果．
【考点精析】根据题目的已知条件，利用函数的最大(小)值与导数的相关知识可以得到问题的答案，需要掌握求函数
在
上的最大值与最小值的步骤：（1）求函数在
内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值．
练习册系列答案
相关题目
