题目内容
已知实数x,y满足不等式组
,则z=(x+4)2+(y-4)2的最大值和最小值分别为( )
|
A、36+16
| ||||
B、4
| ||||
C、36+16
| ||||
D、36+16
|
分析:本题考查的知识点是线性规划,处理的思路为:根据已知的约束条件
,画出满足约束条件的可行域,分析z=(x+4)2+(y-4)2表示的几何意义,结合图象即可给出z=(x+4)2+(y-4)2的取值范围.
|
解答: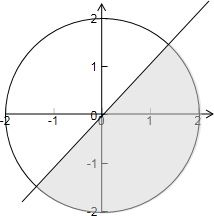 解:约束条件
解:约束条件
对应的平面区域如下图示:
z=(x+4)2+(y-4)2表示可行域内的点(x,y)与点(-4,4)距离的平方,
当(x,y)=(0,0)时取最小值32,
当(x,y)=(
,-
)时取最大值36+16
,
故选A
 解:约束条件
解:约束条件
|
z=(x+4)2+(y-4)2表示可行域内的点(x,y)与点(-4,4)距离的平方,
当(x,y)=(0,0)时取最小值32,
当(x,y)=(
| 2 |
| 2 |
| 2 |
故选A
点评:平面区域的最值问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,则目标函数z=x-y的最大值等于( )
,则目标函数z=x-y的最大值等于( )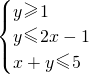 ,则目标函数z=x-y的最大值等于________.
,则目标函数z=x-y的最大值等于________. ,则目标函数z=x-y的最大值等于 .
,则目标函数z=x-y的最大值等于 .