题目内容
已知实数x,y满足不约束条件
,则目标函数z=x-y的最大值等于
|
3
3
.分析:作出平面区域,分析目标函数的几何意义,然后判断目标函数取得最优解的点的坐标,即可求解.
解答: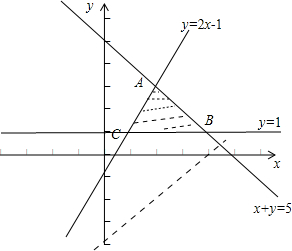 解:由题意作出不等式组表示的平面区域,如图所示
解:由题意作出不等式组表示的平面区域,如图所示
由z=x-y可得y=x-z,则-z表示直线z=x-y在y轴上的截距,截距越小,z越大,
故当直线过点B的时候,会使目标函数取最大值
由
可得B(4,1),此时z最大为z=4-1=3
故答案为:3
 解:由题意作出不等式组表示的平面区域,如图所示
解:由题意作出不等式组表示的平面区域,如图所示由z=x-y可得y=x-z,则-z表示直线z=x-y在y轴上的截距,截距越小,z越大,
故当直线过点B的时候,会使目标函数取最大值
由
|
故答案为:3
点评:本题考查线性规划知识的运用,熟练作出图象是解决问题的关键,属基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 ,则目标函数z=x-y的最大值等于( )
,则目标函数z=x-y的最大值等于( )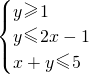 ,则目标函数z=x-y的最大值等于________.
,则目标函数z=x-y的最大值等于________. ,则目标函数z=x-y的最大值等于 .
,则目标函数z=x-y的最大值等于 .