题目内容
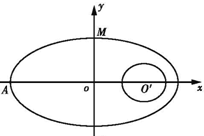 如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为 ,左顶点为A(-4,0).圆O′:
,左顶点为A(-4,0).圆O′: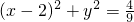
(Ⅰ)求椭圆G的方程;
(Ⅱ)过M(0,1)作圆O′的两条切线交椭圆于E、F,判断直线EF与圆的位置关系,并证明.
解:(Ⅰ)∵椭圆G的离心率为 ,左顶点为A(-4,0)
,左顶点为A(-4,0)
∴
∴c= ,∴b=1
,∴b=1
∴椭圆G的方程为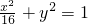 ;
;
(Ⅱ)直线EF与圆O'的相切
设过点M(0,1)与圆O′: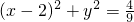 相切的直线方程为:y-1=kx①
相切的直线方程为:y-1=kx①
则 ,即32k2+36k+5=0②,解得
,即32k2+36k+5=0②,解得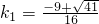 ,
,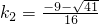
把①代入椭圆方程,消去y可得(16k2+1)x2+32kx=0,则异于零的解为x=-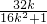
设F(x1,k1x1+1),E(x2,k2x2+1),则x1=- ,x2=-
,x2=-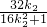
则直线FE的斜率为:kEF= =
=
于是直线FE的方程为:y+ -1=
-1= (x+
(x+ )即y=
)即y= x-
x-
则圆心(2,0)到直线FE的距离d= =
= ,故结论成立.
,故结论成立.
分析:(Ⅰ)利用椭圆G的离心率为 ,左顶点为A(-4,0),建立方程,即可求得椭圆G的方程;
,左顶点为A(-4,0),建立方程,即可求得椭圆G的方程;
(Ⅱ)直线EF与圆O'的相切.设过点M(0,1)与圆相切的直线方程为:y-1=kx,由圆心到直线的距离等于半径求k的值,与椭圆方程联立,表示出E,F和坐标,从而得到EF所在的直线的方程,再探讨圆心到直线的距离和半径的关系.
点评:本题主要是通过圆和椭圆来考查直线和圆,直线和椭圆的位置关系,考查学生的计算能力.
 ,左顶点为A(-4,0)
,左顶点为A(-4,0)∴

∴c=
 ,∴b=1
,∴b=1∴椭圆G的方程为
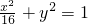 ;
;(Ⅱ)直线EF与圆O'的相切
设过点M(0,1)与圆O′:
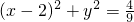 相切的直线方程为:y-1=kx①
相切的直线方程为:y-1=kx①则
 ,即32k2+36k+5=0②,解得
,即32k2+36k+5=0②,解得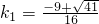 ,
,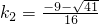
把①代入椭圆方程,消去y可得(16k2+1)x2+32kx=0,则异于零的解为x=-
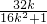
设F(x1,k1x1+1),E(x2,k2x2+1),则x1=-
 ,x2=-
,x2=-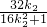
则直线FE的斜率为:kEF=
 =
=
于是直线FE的方程为:y+
 -1=
-1= (x+
(x+ )即y=
)即y= x-
x-
则圆心(2,0)到直线FE的距离d=
 =
= ,故结论成立.
,故结论成立.分析:(Ⅰ)利用椭圆G的离心率为
 ,左顶点为A(-4,0),建立方程,即可求得椭圆G的方程;
,左顶点为A(-4,0),建立方程,即可求得椭圆G的方程;(Ⅱ)直线EF与圆O'的相切.设过点M(0,1)与圆相切的直线方程为:y-1=kx,由圆心到直线的距离等于半径求k的值,与椭圆方程联立,表示出E,F和坐标,从而得到EF所在的直线的方程,再探讨圆心到直线的距离和半径的关系.
点评:本题主要是通过圆和椭圆来考查直线和圆,直线和椭圆的位置关系,考查学生的计算能力.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
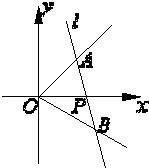 如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB: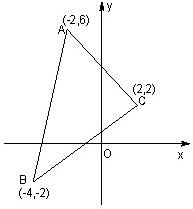 如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求:
如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求: 如图,在直角坐标系中,直线y=6-x与
如图,在直角坐标系中,直线y=6-x与 如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.
如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m. 如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为