题目内容

如图，在直角坐标系中，直线y=6-x与y=
4x
(x＞0)的图象相交于点A、B，设点A的坐标为（x1，y1），那么长为x1，宽为y1的矩形面积和周长分别为
4，12
4，12
．
分析：将直线y=6-x与曲线y=
4
x
(x＞0)联解，可得x+
4
x
=6．由此根据矩形的周长和面积公式，结合曲线y=
4
x
的方程即可算出长为x1，宽为y1的矩形面积和周长．
解答：解：联解
y=6-x
y=
4
x
，得x+
4
x
=6
∵点A（x1，y1）在y=
4
x
(x＞0)的图象上
∴长为x1，宽为y1的矩形面积S=x1y1=x1•
4
x1
=4
周长为2（x1+y1）=2（x1+
4
x1
）=2×6=12
故答案为：4，12
点评：本题给出直线与曲线相交，求矩形的周长和面积．着重考查了直线与曲线的交点、矩形的周长与面积等知识，属于基础题．
练习册系列答案
相关题目
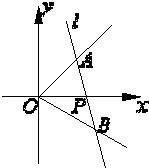精英家教网如图，在直角坐标系中，射线OA：x-y=0（x≥0），OB：
3
x+3y=0（x≥0），
过点P（1，0）作直线分别交射线OA、OB于A、B点．
①当AB的中点为P时，求直线AB的方程；
②当AB的中点在直线y=
1
2
x上时，求直线AB的方程．
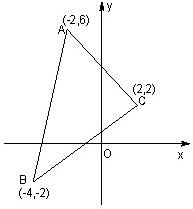精英家教网如图，在直角坐标系中，已知△ABC的三个顶点的坐标，求：
（1）直线AB的一般式方程；
（2）AC边上的高所在直线的斜截式方程．
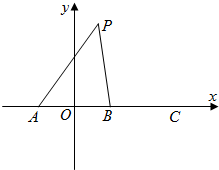精英家教网如图，在直角坐标系中，A，B，C三点在x轴上，原点O和点B分别是线段AB和AC的中点，已知AO=m（m为常数），平面上的点P满足PA+PB=6m．
（1）试求点P的轨迹C1的方程；
（2）若点（x，y）在曲线C1上，求证：点(
x
3
，
y
2
2
)一定在某圆C2上；
（3）过点C作直线l，与圆C2相交于M，N两点，若点N恰好是线段CM的中点，试求直线l的方程．
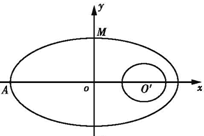如图，在直角坐标系中，中心在原点，焦点在x轴上的椭圆G的离心率为
15
4
，左顶点为A（-4，0）．圆O′：(x-2)2+y2=
4
9

（Ⅰ）求椭圆G的方程；
（Ⅱ）过M（0，1）作圆O′的两条切线交椭圆于E、F，判断直线EF与圆的位置关系，并证明．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网