题目内容
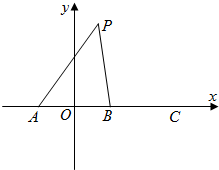 如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.
如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.(1)试求点P的轨迹C1的方程;
(2)若点(x,y)在曲线C1上,求证:点(
| x |
| 3 |
| y | ||
2
|
(3)过点C作直线l,与圆C2相交于M,N两点,若点N恰好是线段CM的中点,试求直线l的方程.
分析:(1)由题意结合椭圆的定义可得点P的轨迹C1是以A,B为焦点的椭圆,且半焦距长c=m,长半轴长a=3m,从而写出C2的方程.
(2)若点(x,y)在曲线C1上,则点的坐标适合曲线的方程:
+
=1.经过转换得x02+y02=m2,从而得出点(
,
)一定在某一圆C2上.
(3)由题意C(3m,0),M(x1,y1),利用因为点N恰好是线段CM的中点,得到N点的坐标,代入C2的方程得方程组,即可解得直线l有且只有一条.
(2)若点(x,y)在曲线C1上,则点的坐标适合曲线的方程:
| x2 |
| 9m2 |
| y2 |
| 8m2 |
| x |
| 3 |
| y | ||
2
|
(3)由题意C(3m,0),M(x1,y1),利用因为点N恰好是线段CM的中点,得到N点的坐标,代入C2的方程得方程组,即可解得直线l有且只有一条.
解答:解:(1)由题意可得点P的轨迹C1是以A,B为焦点的椭圆.…(2分)
且半焦距长c=m,长半轴长a=3m,则C1的方程为
+
=1.…(5分)
(2)若点(x,y)在曲线C1上,则
+
=1.设
=x0,
=y0,则x=3x0,y=2
y0.…(7分)
代入
+
=1,得x02+y02=m2,所以点(
,
)一定在某一圆C2上.
…(10分)
(3)由题意C(3m,0).…(11分)
设M(x1,y1),则x12+y12=m2.…①
因为点N恰好是线段CM的中点,所以N(
,
).代入C2的方程得(
)2+(
)2=m2.…②
联立①②,解得x1=-m,y1=0.…(15分)
故直线l有且只有一条,方程为y=0.…(16分)
(若只写出直线方程,不说明理由,给1分)
且半焦距长c=m,长半轴长a=3m,则C1的方程为
| x2 |
| 9m2 |
| y2 |
| 8m2 |
(2)若点(x,y)在曲线C1上,则
| x2 |
| 9m2 |
| y2 |
| 8m2 |
| x |
| 3 |
| y | ||
2
|
| 2 |
代入
| x2 |
| 9m2 |
| y2 |
| 8m2 |
| x |
| 3 |
| y | ||
2
|
…(10分)
(3)由题意C(3m,0).…(11分)
设M(x1,y1),则x12+y12=m2.…①
因为点N恰好是线段CM的中点,所以N(
| x1+3m |
| 2 |
| y1 |
| 2 |
| x1+3m |
| 2 |
| y1 |
| 2 |
联立①②,解得x1=-m,y1=0.…(15分)
故直线l有且只有一条,方程为y=0.…(16分)
(若只写出直线方程,不说明理由,给1分)
点评:本小题主要考查曲线与方程、圆锥曲线的轨迹问题等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
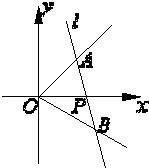 如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB: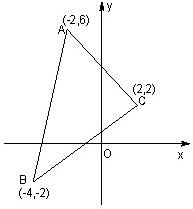 如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求:
如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求: 如图,在直角坐标系中,直线y=6-x与
如图,在直角坐标系中,直线y=6-x与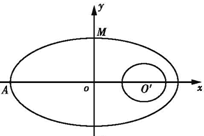 如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为