题目内容
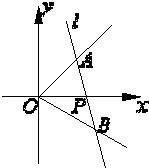 如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB:| 3 |
过点P(1,0)作直线分别交射线OA、OB于A、B点.
①当AB的中点为P时,求直线AB的方程;
②当AB的中点在直线y=
| 1 |
| 2 |
分析:①由题意直线AB的斜率不为0,因为过点P,故可设为:x=my+1,分别与射线OA、OB联立,求出A、B点坐标,因为AB的中点为P,由中点坐标公式列方程求解即可.
②同①求出A、B点坐标,求出中点坐标,因为AB的中点在直线y=
x上,代入求解即可.
②同①求出A、B点坐标,求出中点坐标,因为AB的中点在直线y=
| 1 |
| 2 |
解答:解:①由题意直线AB的斜率不为0,因为过点P,故可设为:x=my+1,
分别与射线OA、OB联立,得A(
,
),B(
,-
)
因为AB的中点为P,由中点坐标公式
-
=0,解得m=
所以直线AB的方程为:2x-(1-
)y-2=0
②由①可知AB的中点M坐标为:(
,
),
因为AB的中点在直线y=
x上,所以
=
,
解得:m=
,所以直线AB的方程为:3x-(3-
)y-3=0
分别与射线OA、OB联立,得A(
| 1 |
| 1-m |
| 1 |
| 1-m |
| ||
m+
|
| 1 | ||
m+
|
因为AB的中点为P,由中点坐标公式
| 1 |
| 1-m |
| 1 | ||
m+
|
1-
| ||
| 2 |
所以直线AB的方程为:2x-(1-
| 3 |
②由①可知AB的中点M坐标为:(
| ||||||||
| 2 |
| ||||||
| 2 |
因为AB的中点在直线y=
| 1 |
| 2 |
| ||||||
| 2 |
| 1 |
| 2 |
| ||||||||
| 2 |
解得:m=
3-
| ||
| 3 |
| 3 |
点评:本题考查两条直线的交点坐标、中点坐标公式及求直线方程问题,考查运算能力.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
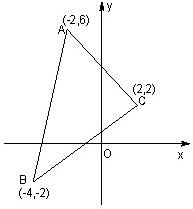 如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求:
如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求: 如图,在直角坐标系中,直线y=6-x与
如图,在直角坐标系中,直线y=6-x与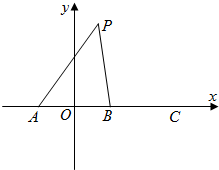 如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.
如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.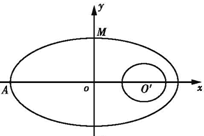 如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为